
Methods & Expertise
The STRUCTURES Cluster of Excellence in Heidelberg aims at a unified approach to understanding how structure, collective phenomena, and complexity emerge in the physical world, mathematics and complex data. To this end we explore new concepts and methods that are also central for finding structures in large datasets, and for realizing new forms of analogue computing. Our research addresses specific, highly topical questions about the formation, role, and detection of structure in a broad range of natural phenomena, from subatomic particles to cosmology, and from fundamental quantum physics to neuroscience.
The major challenge we face in all these questions is that of bridging large scale differences: in all the phenomena we study, physical processes on a wide range of time and length scales combine. While essential for the richness of observed phenomena, this poses enormous challenges for a quantitative analysis. It is the central idea of STRUCTURES that these seemingly very different phenomena admit a common description by unifying fundamental concepts, which we test in a controlled analysis of model systems.
Methods & Competences
Six Methodical Areas – One Connecting Vision
The STRUCTURES Cluster of Excellence is a dynamic and vibrant interdisciplinary environment bringing together experts from diverse fields and methodical areas. We combine leading expertise in three broad methodical areas, namely (A) mathematical theory, comprising the mathematically rigorous study of models, as well as multiscale theory, in particular renormalization group theory, (B) simulation and data analysis, including large-scale numerical computation and data analysis using deep network architectures and scientific visualization, and (C) physical computation, corresponding to synthetic quantum systems.
The unifying and unique aspect of research in STRUCTURES is the combination of methods and the close collaboration of scientists from pure mathematics to experimental physics, which allows us to pursue the research described in the comprehensive projects CP1 to CP7, which could not be addressed by the individual groups in isolation. Compared to other research institutions in the world, and especially other universities in Germany, it is the combination of this expertise that makes Heidelberg an ideal place to do the research envisaged in STRUCTURES.
In the following, we give details on each of the broad methodical areas:
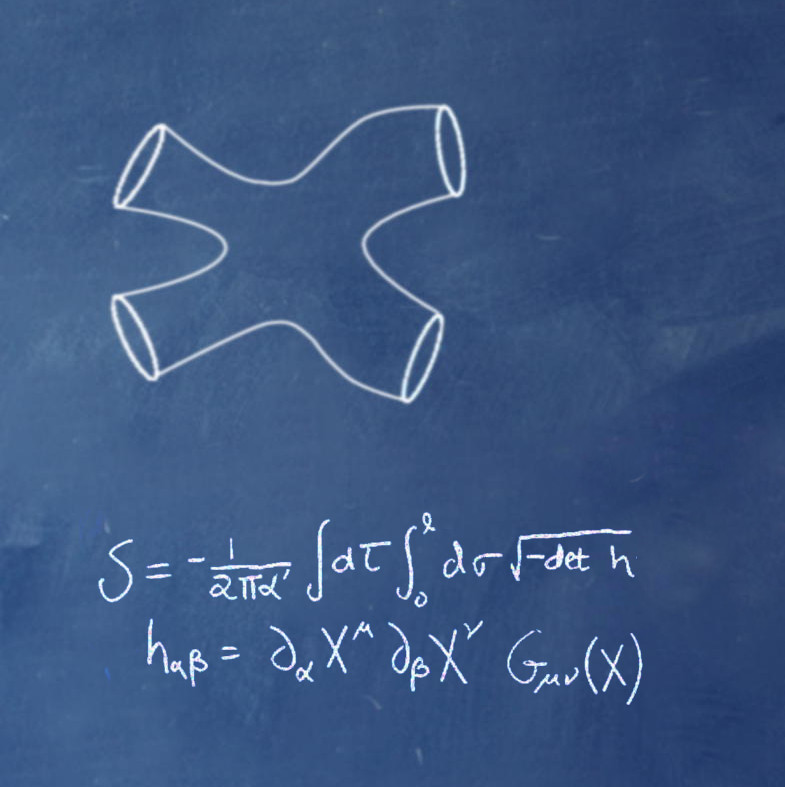
(A) Mathematical Theory
The methods from mathematics and theoretical physics used in the cluster range from pure mathematics, in particular topology and geometry, via analysis, in particular homogenization and analysis of nonlinear partial differential equations (PDE), to field theoretical methods and the renormalization group. The role of mathematics here is to provide proofs whenever this is possible, and guiding principles for theory and for simulation methods, and also to uncover inherent topological and geometric structures and make use of them to answer research question from astronomy to biophysics. Conversely, ideas from theoretical physics provide intuition about new mathematical structures.
Functional integral methods from quantum field theory (QFT) and statistical field theory provide a unifying theoretical framework with almost universal applicability in physics, ranging from the formulation of the standard model of particle physics and its extensions to the study of cold atomic gases, classical statistical systems, averaged models of neuromorphic systems, or cosmology. Nonequilibrium systems, in particular many-body dynamics in which the initial state is not known precisely, but drawn from some probability ensemble, also fall into this very general framework. Field theoretical methods have also been successful in completely different subject areas, e.g., financial mathematics. They have also led to important insights in pure mathematics. A famous example is the identification of knot invariants like the Jones polynomial as Wilson loop expectation values in a Chern-Simons QFT.

(B) Simulation and Data Analysis
Structure formation in nature often involves a wide range of different physical and chemical processes. In STRUCTURES we address selected examples, such as the build-up of galaxies in the early universe, the formation of planets around stars like our Sun, or pattern formation in biological systems. Adequate models for this typically involve tightly coupled PDEs with many degrees of freedom. They combine fluid and gas flows with the dynamics of particles or cell fibers. Their solution requires numerical simulations. Even the largest simulations, which we do at national or European supercomputing centers, can cover only a limited range of spatial or temporal scales. The dynamics on unresolved small scales can only be included via approximative ‘sub-grid’ models, while processes acting on scales above the computational domain can only be included via adequate initial and boundary conditions. This is where methods from field theory and the renormalization group become important. They can give further input and provide the link between simulations on very different scales. Vice versa, the detailed numerical models can be used to test and validate the functional methods. Exploring the close interplay between these complementary approaches is a key aspect of STRUCTURES.
The simulations as well as the experiments in STRUCTURES will produce huge volumes of complex data. For data processing and analysis we have access to a wide portfolio of tools and methods, viz. computationally-intensive calculations of high-order correlation functions, advanced scientific visualization techniques, and innovative machine learning algorithms and deep neural networks. We will also employ topological methods, such as persistent homology. It is one of the goals of this cluster to advance these techniques further and adapt them to the structure-formation problems in the focal point of STRUCTURES.

(C) Physical Computation
Because the models implemented in experiments on synthetic systems are very cleanly realized and their parameters can be controlled very well, they serve to test and rigorously benchmark results obtained by approximate analytical theory and simulations.
It is well known that many-body quantum systems and quantum fields pose very hard challenges to theory and numerical simulation alike. To name but two examples – strong interactions of quantum particles continue to pose an obstacle for analytic approaches based on standard field-theoretical techniques, and numerical simulations often face the so-called fermionic sign problem, which hampers or even prevents importance sampling in probabilistic algorithms. It is likely that the computational complexity of quantum problems is typically nonpolynomial in the number of particles. A second, very important role of synthetic systems is therefore that they can be used to obtain the result for specific model systems by physical computation – a sequence of steps including preparation, time evolution and measurement that replaces a numerical or analytical computation. This opens the possibility of creating hybrid computational devices, where part of the calculation is done on a digital computer, and another part is done using the synthetic system.
In a similar vein, the neuromorphic hardware can be used to test ideas about how biological brains function and to study emergent phenomena in well-specified systems of neurons, but it can also be applied to machine learning problems, since it is a network that can be trained, and that, among other things, can be configured to realize standard models of non-spiking networks as a special case.
