CP Overview
Select a CP to highlight it.
Comprehensive Projects
The comprehensive projects (CP) define the main research lines of the cluster. They have a broad scope and address the key questions of STRUCTURES, combining the methods coming from the different methodical areas of the cluster.
The following diagram shows the members of STRUCTURES, their home institutes, the three methodical areas (mathematical theory in red, simulation and data analysis in green, physical computation in blue) and in the center, the comprehensive projects, which connect the different areas.
CP1. Cosmic Structure Formation: Reionizing the Universe with the First Stars and Galaxies
In its relatively early stages, the universe was almost perfectly uniform and its dynamics was dominated by gravity. Today, it is highly structured and its evolution is governed by a multitude of physical processes coupling dark matter, baryons, and radiation on a wide range of spatial and temporal scales. In its evolution towards increasing complexity, the formation of the first stars and galaxies marks a primary transition event. Their light ended the so-called 'dark ages', defining the epoch of cosmic reionization, less than a billion years after the big bang. Our goal is to identify and characterize the primary sources of cosmic reionization, and make detailed predictions for future astronomical observations and surveys. We will investigate whether the large-scale evolution can be described in terms of a non-equilibrium phase transition, and if yes, determine the relevant order parameter. Our approach combines multiscale numerical simulations, data analysis techniques, and functional methods in the form of kinetic field theory.
CP2. From Dust to Planets: Facing the Multi-Scale Challenge
Rocky planets, such as our Earth, form from cosmic dust in protoplanetary disks around young stars. Our current understanding of this process contains a gap, connected to the so-called metre-size barrier in the formation of planetesimals. The questions we address are: Can this gap be closed by a combination of turbulence, coagulation, and gravitational dynamics? And can we thus complete our understanding of how complex structures, such as the diverse exoplanetary systems known today, formed from initially nearly homogeneous distributions of gas and dust? The extraordinary difficulty of this problem calls for new computational methods, which we will develop in the areas of particle- and fluid-based simulations, particle distribution function solvers, functional methods based on kinetic field theory, and their mutual interconnections.
CP3. From Molecules to Cells and Tissue: Coupling Continuous and Discrete Structures
The fundamental principles underlying the function of cellular and tissue systems are not only essential for the life sciences, but also for new fields at the interface with medicine and materials science. CP3 builds on recent advances in the life sciences, which have revealed that spatial structure is much more important than formerly appreciated, for example for the compartmentalization of biological function and in the context of cell and tissue mechanics. Very often spatial structures form as discrete or lower-dimensional components in a continuous background. Combining our expertise in life sciences, biophysics, mathematical analysis and scientific computation, we will advance continuum models and their finite element discretizations for selected model systems of this kind, in particular for fibre systems that dynamically grow or reorganize in the cell, and for groups of specialized cells that emerge in the context of a growing tissue.
CP4. Quantum Structure and Dynamics: Fundamental and Emergent
The quantum world has many features that are remote from our everyday experience and appear counterintuitive, yet quantum structures are fundamental to the stability of our macroscopic world and determine most of the natural phenomena around us. They are also the reason why modern technologies, in particular all electronic devices, work. CP4 investigates the role of the most important abstract quantum structures, in particular quantum coherence and entanglement, for physical structures and many-body dynamics. How strongly do entanglement and quantum coherence influence the emergent dynamics of many-body systems, and does this imply a characteristically non-classical way of emergence of material structures? We address these questions by a combination of field theoretic functional methods, state-of-the-art simulation methods, mathematical proofs, and precision experiments, among them the new Heidelberg Quantum Architecture.
CP5. Quantum Systems and Neural Networks: Computation in Physical Structures
Quantum systems and large networks of spiking neurons both contain subtle nonlocal connections, caused by entanglement in the quantum case, and by long-range synaptic links in the neural case. Research in CP5 explores common layers of complexity of these seemingly very different systems, and their potential for novel ways of computation. How can these new types of computers be related to Turing machines? We combine field theoretical methods with precision experiments on cold quantum gases and on neuromorphic hardware. As a completely new approach, the interface will be implemented physically by connecting the Heidelberg Quantum Architecture to the neuromorphic computing facility BrainScaleS.
CP6. Networks and Machine Learning: Mathematical Structures
Machine learning has become a spectacularly successful tool. Its product, the 'learned machine', is an emergent structure, which is not completely understood. Research in CP6 addresses questions both of fundamental and of practical importance: How can we characterize the underlying structure of most natural data that makes their mathematical representation occupy only a tiny part of the potentially available space? How can we improve training and representation to optimize detection of structure in data on a large scale? Our research brings together expertise in network theory, image recognition, and topology, as well as input from statistical mechanics.
CP7. Quantum Geometry and Topological Methods in Physics: From Spectral Networks to Intersection Homology
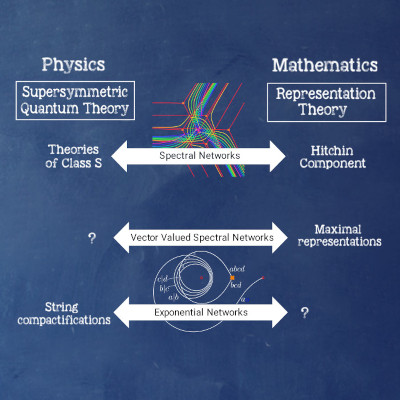
The close interaction of mathematics and physics has been a long success story. Recently, physical dualities linking seemingly distant theories have lead to unexpected breakthroughs in mathematics. In CP7 we explore connections between supersymmetric quantum field theories and modern differential and algebraic geometry with the aim to provide a (more) complete picture of these correspondences. We investigate and refine geometric and topological structures that play a key role in understanding emergent phenomena in physics, as well as biology, and support their application in the other comprehensive and exploratory projects of the cluster.