
Exploratory Projects
In addition to the comprehensive projects (CP), the exploratory projects (EP) play an important role for the functioning and the development of the cluster. The format of EPs is completely flexible. Their scope ranges from focused projects that pursue ideas not (yet) represented in the CPs, collaborations that establish new links between researchers in different fields, joint workshop and group activities to explore and develop new interdisciplinary topics, to projects that link the cluster to other parts of academia.
Twice a year, we call for EP proposals to be submitted to the steering board of the cluster. Up to now, we have selected 67 EPs, which have been initiating a lot of activity in the cluster, providing innovative ideas and freshening our research.
Call Winter 2024/25
67. Tensor Models and Gravitational Universality Classes
Astrid Eichhorn, Razvan Gurau, Jan Pawlowski

Just like water only appears to be a continuous fluid, but is actually made up of discrete building blocks (the molecules), spacetime could also be made up of discrete building blocks. A continuum, physical spacetime can emerge from such building blocks at a phase transition, where many building blocks come together to give rise to extended geometric spacetime structures.
This project will search for such a phase transition in tensor models, which are one proposal for a description of spacetime in terms of discrete building blocks. Our method will involve a discrete version of the Renormalization Group (RG), which enables us to study the emergent large-scale behaviour from the interactions of the microscopic building blocks. This project connects to several themes within the broader context of STRUCTURES by studying how the geometric structure of spacetime may ultimately emerge from a discrete setting.
Just like water only appears to be a continuous fluid, but is actually made up of discrete building blocks (the molecules), spacetime could also be made up of discrete building blocks. A continuum, physical spacetime can emerge from such building blocks at a phase transition, where many building blocks come together to give rise to extended geometric spacetime structures.
This project will search for such a phase transition in tensor models, which are one proposal for a description of spacetime in terms of discrete building blocks. Our method will involve a discrete version of the (...) Renormalization Group (RG), which enables us to study the emergent large-scale behaviour from the interactions of the microscopic building blocks. This project connects to several themes within the broader context of STRUCTURES by studying how the geometric structure of spacetime may ultimately emerge from a discrete setting.
66. Inferring Drivers in Non-Autonomous Astrophysical Dynamical Systems
Tobias Buck, Daniel Durstewitz, Hubert Klahr
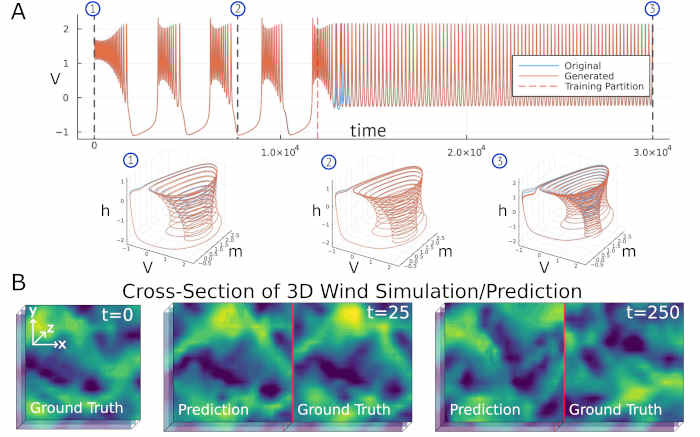
Modelling the evolution of astrophysical phenomena is particularly challenging for non-autonomous systems with drifting dynamics due to external driving forces. This EP leverages recent deep learning breakthroughs to infer these unknown forces from real or simulated non-stationary data. Building on previous dynamical system reconstruction (DSR) models, the project extends these methods by integrating time-dependent, domain-specific feature vectors to capture critical control parameters. The research involves validating the approach on simulated model systems and pre-training on extensive simulated datasets, before applying it to complex astrophysical scenarios, like planet-forming disks and the interstellar medium. By jointly inferring the dynamics and functional form of the time-dependent forcing from non-snapshot data, the project aims to overcome limitations of traditional DSR techniques. This cross-disciplinary effort bridges machine learning and astrophysics, opening new paths for analyzing phase transitions and tipping points in non-ergodic systems.
Modelling the evolution of astrophysical phenomena is particularly challenging for non-autonomous systems with drifting dynamics due to external driving forces. This EP leverages recent deep learning breakthroughs to infer these unknown forces from real or simulated non-stationary data. Building on previous dynamical system reconstruction (DSR) models, the project extends these methods by integrating time-dependent, domain-specific feature vectors to capture critical control parameters. The research involves validating the approach on simulated model systems and pre-training on extensive (...) simulated datasets, before applying it to complex astrophysical scenarios, like planet-forming disks and the interstellar medium. By jointly inferring the dynamics and functional form of the time-dependent forcing from non-snapshot data, the project aims to overcome limitations of traditional DSR techniques. This cross-disciplinary effort bridges machine learning and astrophysics, opening new paths for analyzing phase transitions and tipping points in non-ergodic systems.
65. Building an RG Quantum Simulator – Exploring Functional Renormalisation Group Flows Through Physics-Derived Regulators
Xin Chen, Selim Jochim, Richard Schmidt, Manfred Salmhofer, Maximilian Rieger
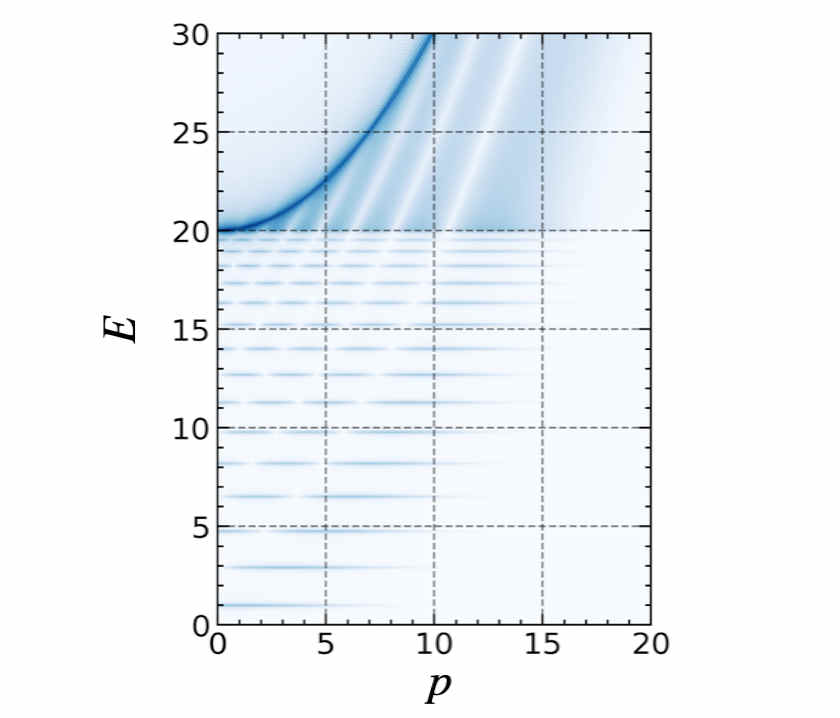
The renormalization group (RG) is a powerful tool to study physical systems exhibiting complex structures across different scales. Starting from a microscopic description of the theory, the RG yields a flow of effective theories capturing the system's behaviour at successively more macroscopic scales. This allows the study of emergent collective phenomena and quantum phases of matter. Formally, the RG flow is obtained by solving a complex functional differential equation for an effective flowing action describing how correlations between particles emerge. However, the competition of different correlations during the flow typically makes a numerical solution extremely difficult. To advance, it would be useful to employ nature itself to obtain the RG flow of some observable quantity directly in controlled quantum experiments. The result could serve as a benchmark for different approximation schemes employed in theoretical many-body physics. This EP explores how an ultracold atom experiment can serve as such a platform. By utilizing a confining potential (e.g., a harmonic trap), an infrared regulator can be implemented, gapping out the energy spectrum of the theory. Adiabatically removing the trap then becomes equivalent to an RG flow. We investigate the applicability of this approach to problems such as the two- and three-body problem and the emergence of superfluid pairing in a trapped, mesoscopic, fermionic gas.
The renormalization group (RG) is a powerful tool to study physical systems exhibiting complex structures across different scales. Starting from a microscopic description of the theory, the RG yields a flow of effective theories capturing the system's behaviour at successively more macroscopic scales. This allows the study of emergent collective phenomena and quantum phases of matter. Formally, the RG flow is obtained by solving a complex functional differential equation for an effective flowing action describing how correlations between particles emerge. However, the competition of different (...) correlations during the flow typically makes a numerical solution extremely difficult. To advance, it would be useful to employ nature itself to obtain the RG flow of some observable quantity directly in controlled quantum experiments. The result could serve as a benchmark for different approximation schemes employed in theoretical many-body physics. This EP explores how an ultracold atom experiment can serve as such a platform. By utilizing a confining potential (e.g., a harmonic trap), an infrared regulator can be implemented, gapping out the energy spectrum of the theory. Adiabatically removing the trap then becomes equivalent to an RG flow. We investigate the applicability of this approach to problems such as the two- and three-body problem and the emergence of superfluid pairing in a trapped, mesoscopic, fermionic gas.
64. Building Fractional Quantum Hall States Atom-by-Atom
Selim Jochim, Richard Schmidt, Matthias Weidemüller, Maciej Gałka
When exposed to very strong magnetic fields, charged particles begin to move in highly coordinated ways, leading to the Fractional Quantum Hall (FQH) effect at extremely low temperatures. In this state, electrons move collectively, swirling around one another in a synchronized pattern. This behaviour is driven by the Lorentz force, which bends the path of charged particles in a magnetic field.
Interestingly, a similar effect can be created using neutral atoms by rotating the entire system. In this case, the atoms experience the Coriolis force – the same force you feel when trying to walk straight on a spinning carousel. This force is analogous to the Lorentz force and gives rise to similar dynamics.
In this project, we use rotating clouds of neutral atoms to simulate quantum Hall physics, allowing us to explore these exotic states of matter beyond what is possible in conventional materials. In particular, the tunability of interactions allows us to bind fermionic atoms into bosonic molecules, effectively changing quantum statistics of particles in the system. This enables the study of quantum phase transitions between different types of quantum Hall states and will provide new insights into the nature of strongly correlated quantum matter.
When exposed to very strong magnetic fields, charged particles begin to move in highly coordinated ways, leading to the Fractional Quantum Hall (FQH) effect at extremely low temperatures. In this state, electrons move collectively, swirling around one another in a synchronized pattern. This behaviour is driven by the Lorentz force, which bends the path of charged particles in a magnetic field.
Interestingly, a similar effect can be created using neutral atoms by rotating the entire system. In this case, the atoms experience the Coriolis force – the same force you feel when trying to walk (...) straight on a spinning carousel. This force is analogous to the Lorentz force and gives rise to similar dynamics.
In this project, we use rotating clouds of neutral atoms to simulate quantum Hall physics, allowing us to explore these exotic states of matter beyond what is possible in conventional materials. In particular, the tunability of interactions allows us to bind fermionic atoms into bosonic molecules, effectively changing quantum statistics of particles in the system. This enables the study of quantum phase transitions between different types of quantum Hall states and will provide new insights into the nature of strongly correlated quantum matter.
63. Sampling in High Dimensions – Using Intrinsic Structures to Tame Complexity
Friederike Ihssen, Jan M. Pawlowski, Björn Malte Schäfer, Robert Scheichl
Sampling, i.e. the generation of random numbers with defined statistical properties, from complex, high-dimensional distributions is a central issue in physics, applied mathematics and statistics alike. In this project we address the sampling task comprehensively by drawing on fundamental links between efficient sampling approaches in lattice field theories and statistical mechanics, non-parametric Bayesian statistics, and learning-based inference of function-valued parameters. Technically, we make progress by devising sampling approaches for complex high-dimensional distributions that exploit low-dimensional structures in the form of effective theories, surrogates or reduced-order models in fast-mixing Markov chains, generative models, and approximate cumulants. Scientifically, the project evolves around inference in field theories on different scales with renormalisation group methods, the theoretical foundation of multilevel sampling; and around regularisation mechanisms for inference in cosmology.
In summary, we aim at taming model complexity in inference problems across three different disciplines, embedding machine-learning methods for this purpose into a comprehensive conceptual framework. We hope to shed some light into the question of scale-dependence of physical information hidden in data, by joining ideas of renormalisation and regularisation from theoretical physics, data tempering and delayed acceptance in PDE-constrained inference, and Bayesian partition functions for inference in cosmology. With applications ranging from effective field theories in QFT, PDE inference (e.g., pollutant transport in soil) and large-scale structure reconstructions in cosmology, the project focuses on highly topical questions and combines state-of-the-art methods across disciplines.
Sampling, i.e. the generation of random numbers with defined statistical properties, from complex, high-dimensional distributions is a central issue in physics, applied mathematics and statistics alike. In this project we address the sampling task comprehensively by drawing on fundamental links between efficient sampling approaches in lattice field theories and statistical mechanics, non-parametric Bayesian statistics, and learning-based inference of function-valued parameters. Technically, we make progress by devising sampling approaches for complex high-dimensional distributions that exploit (...) low-dimensional structures in the form of effective theories, surrogates or reduced-order models in fast-mixing Markov chains, generative models, and approximate cumulants. Scientifically, the project evolves around inference in field theories on different scales with renormalisation group methods, the theoretical foundation of multilevel sampling; and around regularisation mechanisms for inference in cosmology.
In summary, we aim at taming model complexity in inference problems across three different disciplines, embedding machine-learning methods for this purpose into a comprehensive conceptual framework. We hope to shed some light into the question of scale-dependence of physical information hidden in data, by joining ideas of renormalisation and regularisation from theoretical physics, data tempering and delayed acceptance in PDE-constrained inference, and Bayesian partition functions for inference in cosmology. With applications ranging from effective field theories in QFT, PDE inference (e.g., pollutant transport in soil) and large-scale structure reconstructions in cosmology, the project focuses on highly topical questions and combines state-of-the-art methods across disciplines.
Call Winter 2023/24
62. Resource-Efficient Modelling of Astrophysical Photo-Thermo-Chemistry Using Scientific Machine Learning
Tobias Buck, Ralf Klessen, Jakob Zech

Modelling complex chemical reactions in hydrodynamical simulations is essential for understanding galaxy formation and other astrophysical phenomena. Traditional methods for simulating these reactions are computationally demanding, often consuming up to half of the total simulation time. This EP combines expertise from physics, mathematics and computer science to develop cutting-edge scientific machine learning methods that significantly reduce computational costs while preserving accuracy. The project leverages advanced methods such as deep operator learning and neuralODEs to efficiently solve high-dimensional, coupled, non-linear ordinary differential equations (ODEs), and couples them to existing astrophysical radiation-hydrodynamical codes such as AREPO – which is actively used within STRUCTURES. This innovative approach to astrochemistry enables the execution of new galaxy formation simulations that will offer insights into the chemo-dynamical structures from the smallest interstellar scales to the largest scales of the circum- and inter-galactic medium. The project establishes new connections between groups within STRUCTURES and aims to open up new possibilities for solving complex parametric ODEs and potentially also partial differential equation (PDE) systems, as well as new avenues to study galaxy formation.
Modelling complex chemical reactions in hydrodynamical simulations is essential for understanding galaxy formation and other astrophysical phenomena. Traditional methods for simulating these reactions are computationally demanding, often consuming up to half of the total simulation time. This EP combines expertise from physics, mathematics and computer science to develop cutting-edge scientific machine learning methods that significantly reduce computational costs while preserving accuracy. The project leverages advanced methods such as deep operator learning and neuralODEs to efficiently (...) solve high-dimensional, coupled, non-linear ordinary differential equations (ODEs), and couples them to existing astrophysical radiation-hydrodynamical codes such as AREPO – which is actively used within STRUCTURES. This innovative approach to astrochemistry enables the execution of new galaxy formation simulations that will offer insights into the chemo-dynamical structures from the smallest interstellar scales to the largest scales of the circum- and inter-galactic medium. The project establishes new connections between groups within STRUCTURES and aims to open up new possibilities for solving complex parametric ODEs and potentially also partial differential equation (PDE) systems, as well as new avenues to study galaxy formation.
61. Transformers for Out-of-Domain Generalization in Dynamical Systems
Daniel Durstewitz, Stefan Riezler, Georgia Koppe
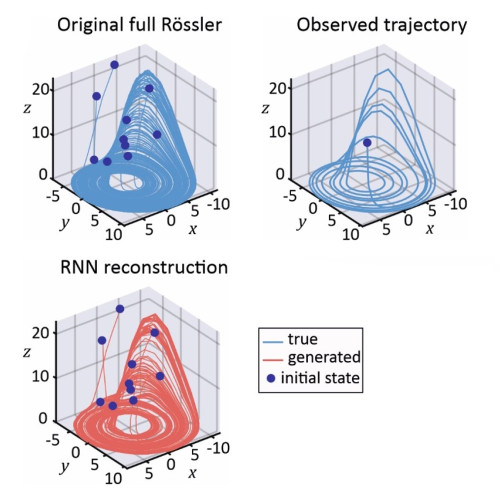
How can we predict the behaviour of complex dynamical systems – such as the climate or the human brain – when they enter entirely new, previously unseen dynamical regimes? Ideally, one would like to have models that are able to generalize across the entire state space of a system, like predicting sleep-stage brain activity after being trained on awake-state data only. However, the state space often segregates into regions of different temporal behaviours, associated with topological changes in the dynamics. Such a topological change, for instance, may occur in a climate system that crossed a tipping point. In general, predicting a system’s dynamics across such changes, known as out-of-domain (OOD) generalization, represents a major challenge. However, recent advances in large language models (LLMs) based on Transformers have shown remarkable generalization abilities, so-called zero-shot and in-context learning where models can handle new problem settings without requiring re-training. This project explores on the one hand whether in-context learning also works for topological OOD generalization in dynamical systems; and on the other hand, whether dynamical systems theory can help explaining the generalization capabilities seen in Transformers. By bridging these fields, the research could open new pathways for understanding and predicting the behaviour of complex, temporally evolving systems.
How can we predict the behaviour of complex dynamical systems – such as the climate or the human brain – when they enter entirely new, previously unseen dynamical regimes? Ideally, one would like to have models that are able to generalize across the entire state space of a system, like predicting sleep-stage brain activity after being trained on awake-state data only. However, the state space often segregates into regions of different temporal behaviours, associated with topological changes in the dynamics. Such a topological change, for instance, may occur in a climate system that crossed (...) a tipping point. In general, predicting a system’s dynamics across such changes, known as out-of-domain (OOD) generalization, represents a major challenge. However, recent advances in large language models (LLMs) based on Transformers have shown remarkable generalization abilities, so-called zero-shot and in-context learning where models can handle new problem settings without requiring re-training. This project explores on the one hand whether in-context learning also works for topological OOD generalization in dynamical systems; and on the other hand, whether dynamical systems theory can help explaining the generalization capabilities seen in Transformers. By bridging these fields, the research could open new pathways for understanding and predicting the behaviour of complex, temporally evolving systems.
60. Multi-scale Procedural Ly-α Modelling for Cosmic Structure Inference
Dylan Nelson
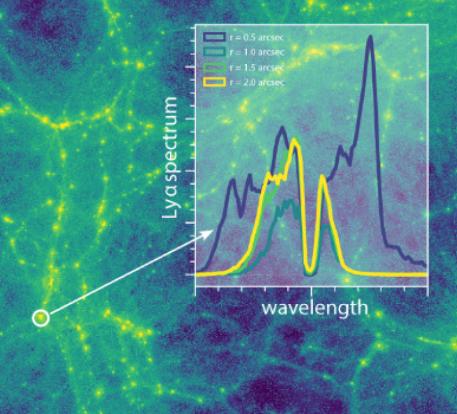
The Ly-α emission line of neutral hydrogen is one of the brightest tracers of galaxies and large-scale structures in the Universe. It can be used to detect distant, young, star-forming galaxies, to constrain cosmological parameters, the progress of cosmic reionization and even to detect the “cosmic web” of large-scale structure. However, the Ly-α line is extraordinarily difficult to interpret due to its resonant nature and the fact that Ly-α photons are scattered many times before escaping, causing significant distortions in both their position and frequency. This radiative transfer process is further complicated by the clumping of hydrogen gas on small scales, necessitating advanced computational techniques to model Ly-α emission across a range of scales. Although state-of-the-art high-resolution hydrodynamical simulations, like IllustrisTNG, offer valuable insights, they cannot fully capture the impact of sub-resolution structures. This EP, which is a natural extension of STRUCTURES’ Comprehensive Project CP1 (Cosmic Structure Formation), focuses on developing new numerical techniques and algorithms to efficiently incorporate the impact of sub-resolution structure into radiative transfer codes. By bridging gaps in current models, this research aims to improve our ability to study cosmic reionization and to unlock the full potential of Ly-α emission as a tool for cosmic discovery.
The Ly-α emission line of neutral hydrogen is one of the brightest tracers of galaxies and large-scale structures in the Universe. It can be used to detect distant, young, star-forming galaxies, to constrain cosmological parameters, the progress of cosmic reionization and even to detect the “cosmic web” of large-scale structure. However, the Ly-α line is extraordinarily difficult to interpret due to its resonant nature and the fact that Ly-α photons are scattered many times before escaping, causing significant distortions in both their position and frequency. This radiative transfer (...) process is further complicated by the clumping of hydrogen gas on small scales, necessitating advanced computational techniques to model Ly-α emission across a range of scales. Although state-of-the-art high-resolution hydrodynamical simulations, like IllustrisTNG, offer valuable insights, they cannot fully capture the impact of sub-resolution structures. This EP, which is a natural extension of STRUCTURES’ Comprehensive Project CP1 (Cosmic Structure Formation), focuses on developing new numerical techniques and algorithms to efficiently incorporate the impact of sub-resolution structure into radiative transfer codes. By bridging gaps in current models, this research aims to improve our ability to study cosmic reionization and to unlock the full potential of Ly-α emission as a tool for cosmic discovery.
59. Exploring Quantum Gravity With Ultracold Atoms
Francesco Gozzini, Lavinia Heisenberg, Markus Oberthaler

In the quest for developing a cogent and comprehensive framework for quantum gravity, the absence of direct experimental data stands as one of the main obstacles, limiting our understanding. At the same time, theoretical physics continues to grapple with applying quantum theory prescriptions to Einstein's theory of General Relativity (GR), prompting exploration of alternative formulations that may simplify this unification. It was shown that GR can be represented in a fully equivalent and simpler fashion when gravity is attributed to a geometric structure known as non-metricity rather than curvature. Meanwhile, in experimental physics, quantum simulators have emerged as a promising tool for probing complex quantum systems. A new platform using a two-dimensional Bose-Einstein condensate (BEC) offers exceptional control over trap configurations and interaction strengths, enabling the simulation of gravitational effects in a laboratory setting. In a collaboration between experimental and theoretical physicists, researchers in this EP will implement analogues of quantum gravitational effects, such as superposition, entanglement, and discrete geometry, into the condensate. They will also extend the canonical quantization approach from Loop Quantum Gravity to theories incorporating non-metricity, and investigate bouncing cosmologies, a common prediction of many quantum gravity theories.
In the quest for developing a cogent and comprehensive framework for quantum gravity, the absence of direct experimental data stands as one of the main obstacles, limiting our understanding. At the same time, theoretical physics continues to grapple with applying quantum theory prescriptions to Einstein's theory of General Relativity (GR), prompting exploration of alternative formulations that may simplify this unification. It was shown that GR can be represented in a fully equivalent and simpler fashion when gravity is attributed to a geometric structure known as non-metricity rather than (...) curvature. Meanwhile, in experimental physics, quantum simulators have emerged as a promising tool for probing complex quantum systems. A new platform using a two-dimensional Bose-Einstein condensate (BEC) offers exceptional control over trap configurations and interaction strengths, enabling the simulation of gravitational effects in a laboratory setting. In a collaboration between experimental and theoretical physicists, researchers in this EP will implement analogues of quantum gravitational effects, such as superposition, entanglement, and discrete geometry, into the condensate. They will also extend the canonical quantization approach from Loop Quantum Gravity to theories incorporating non-metricity, and investigate bouncing cosmologies, a common prediction of many quantum gravity theories.
58. Exploring the Universe with Radio Astronomy and AI
Caroline Heneka, Lara Alegre, Vrund Patel

New radio telescopes, most prominently the Square Kilometre Array (SKA), revolutionize our understanding of galaxy evolution and cosmology by mapping >50% of the observable Universe. Already now, SKA pathfinder experiments such as LOFAR resolve millions of radio sources (galaxies and active galactic nuclei) from present time to a few 100 million years after the Big Bang. The size (raw data rates of TB/s) and complexity (highly non-Gaussian signals) of this data pose a challenge for classical inference methods. This EP therefore focuses on optimal inference of both astrophysics and fundamental physics based on modern amortized inference with machine learning. Extending the scope of CP1 Cosmic Structure Formation to radio mappings, this project closes the gap between machine learning methods successfully trained on simulations and present-day pathfinder observations, in order to learn about key parameters of structure formation such as the dark matter density parameter and the biasing of galaxies against dark matter.
New radio telescopes, most prominently the Square Kilometre Array (SKA), revolutionize our understanding of galaxy evolution and cosmology by mapping >50% of the observable Universe. Already now, SKA pathfinder experiments such as LOFAR resolve millions of radio sources (galaxies and active galactic nuclei) from present time to a few 100 million years after the Big Bang. The size (raw data rates of TB/s) and complexity (highly non-Gaussian signals) of this data pose a challenge for classical inference methods. This EP therefore focuses on optimal inference of both astrophysics and fundamental (...) physics based on modern amortized inference with machine learning. Extending the scope of CP1 Cosmic Structure Formation to radio mappings, this project closes the gap between machine learning methods successfully trained on simulations and present-day pathfinder observations, in order to learn about key parameters of structure formation such as the dark matter density parameter and the biasing of galaxies against dark matter.
57. Modelling Superfluid Dark Matter Using Cold Atoms
David Maibach, Nicolò Defenu, Markus Oberthaler, Manfred Salmhofer
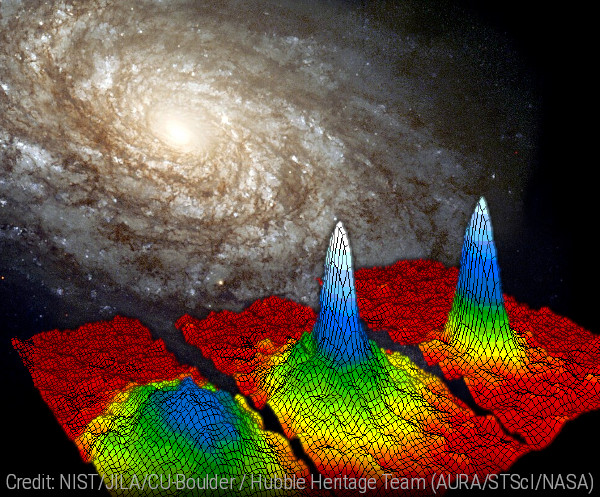
Dark Matter remains one of the most profound enigmas in modern cosmology. Despite a wealth of observational data demonstrating its effects on both small- and large-scale structures within galaxies and galaxy clusters, there is still no comprehensive theoretical framework that unifies these effects in a "natural" way. This project aims to address this gap by applying methodologies and phenomena from condensed matter physics. Specifically, we hypothesize that Dark Matter behaves as a Bose-Einstein condensate at the tricritical point, a state it naturally gravitates toward through the process of self-organized criticality. This approach provides a coherent theoretical model for the observed phenomena. By studying such a condensate within a cosmological context, we hope to shed new light on the mysteries of Dark Matter and potentially Dark Energy.
Dark Matter remains one of the most profound enigmas in modern cosmology. Despite a wealth of observational data demonstrating its effects on both small- and large-scale structures within galaxies and galaxy clusters, there is still no comprehensive theoretical framework that unifies these effects in a "natural" way. This project aims to address this gap by applying methodologies and phenomena from condensed matter physics. Specifically, we hypothesize that Dark Matter behaves as a Bose-Einstein condensate at the tricritical point, a state it naturally gravitates toward through the process of (...) self-organized criticality. This approach provides a coherent theoretical model for the observed phenomena. By studying such a condensate within a cosmological context, we hope to shed new light on the mysteries of Dark Matter and potentially Dark Energy.
56. Invariants of Persistent Stratified Homotopy Types
Lukas Waas, Bernadette Jana Stolz-Pretzer, Markus Banagl
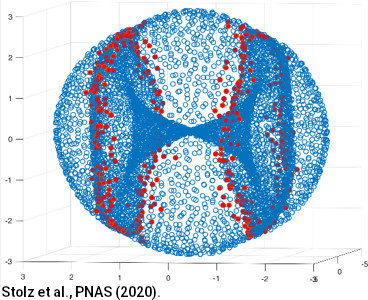
In real-world applications, spatial data is often noisy, complex, and - most importantly for this project - highly heterogeneous. Often, such heterogeneity turns out to be an important feature revealing underlying information. For instance, such a heterogeneous data set might consist of spatial coordinates of tumour cells as well as various immune cell types whose local interactions can be prognostic of disease progress or treatment outcome. In the field of topology, such a decomposition of a space into disjoint pieces is often called a stratification. The way these pieces interact is encoded in an object called the stratified homotopy type, which this EP leverages to capture and quantify key topological features in intrinsically stratified data sets.
In real-world applications, spatial data is often noisy, complex, and - most importantly for this project - highly heterogeneous. Often, such heterogeneity turns out to be an important feature revealing underlying information. For instance, such a heterogeneous data set might consist of spatial coordinates of tumour cells as well as various immune cell types whose local interactions can be prognostic of disease progress or treatment outcome. In the field of topology, such a decomposition of a space into disjoint pieces is often called a stratification. The way these pieces interact is encoded (...) in an object called the stratified homotopy type, which this EP leverages to capture and quantify key topological features in intrinsically stratified data sets.
Call Summer 2023
55. Research Internship (KFT)
Matthias Bartelmann, Olcay Biyikli
This EP allowed a female Turkish BSc student, Ms. Olcay Bıyıklı, to visit Heidelberg and the STRUCTURES community for a summer research internship lasting 2.5 months. During this time, Ms. Bıyıklı studied the foundations of kinetic field theory (KFT) and its application to cosmology. In the course of the project, she got as far as learning about the Hubbard-Stratonovich transform of the generating functional of KFT and its possible advantages in the cosmological context. She gained insight into some of the research topics of STRUCTURES and advanced methods of statistical field theory for non-equilibrium systems. This EP was closely related to CP1 ("Cosmic Structure Formation") and CP2 ("From Dust to Planets") as well as the EP "From Koopman-von Neumann to Structure Formation".
This EP allowed a female Turkish BSc student, Ms. Olcay Bıyıklı, to visit Heidelberg and the STRUCTURES community for a summer research internship lasting 2.5 months. During this time, Ms. Bıyıklı studied the foundations of kinetic field theory (KFT) and its application to cosmology. In the course of the project, she got as far as learning about the Hubbard-Stratonovich transform of the generating functional of KFT and its possible advantages in the cosmological context. She gained insight into some of the research topics of STRUCTURES and advanced methods of statistical field theory for (...) non-equilibrium systems. This EP was closely related to CP1 ("Cosmic Structure Formation") and CP2 ("From Dust to Planets") as well as the EP "From Koopman-von Neumann to Structure Formation".
54. Long-Range Interaction and Machine Learning
Felipe Attanasio, Marc Bauer, Nicolò Defenu, Jan Horak, Friederike Ihssen, Ullrich Köthe, Jan M. Pawlowski, Franz R. Sattler
This EP investigates how we can use machine learning (ML) techniques in long-range interacting physical systems to unlock new insights. Long-range interactions, where forces extend over large distances, are of particular interest, since they create unusual physical behaviours like fast information spread and long-lasting states. To describe these complex systems, we use mathematical tools like the functional renormalization group (fRG) and simulations on a grid (lattice models). These tools provide data, which can be analysed by machine learning models to better understand the relevant dynamical components of the system. Furthermore, the data can be used to train ML models, like those used in language models (e.g., GPT), to emulate these interactions. By combining physics and ML, we hope to improve our understanding of such complex, multi-scale data and behaviours!
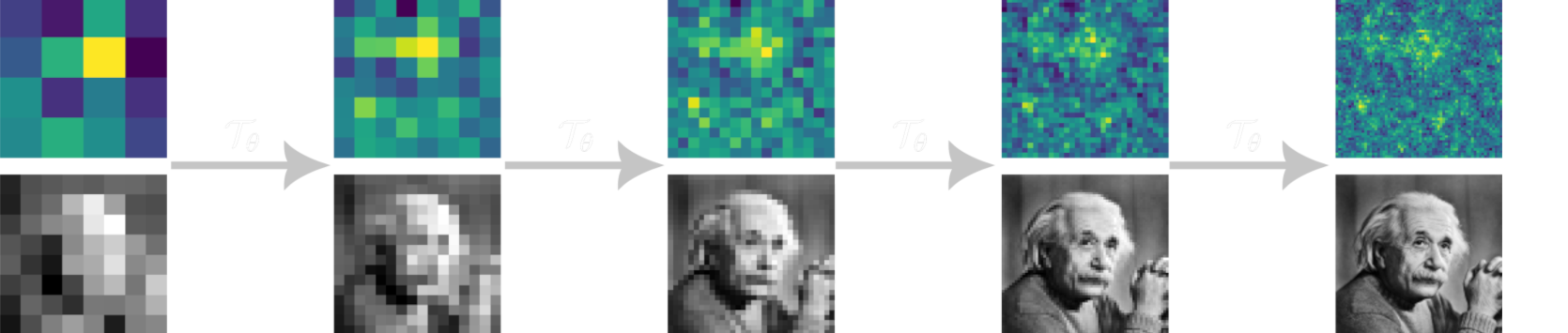 This EP investigates how we can use machine learning (ML) techniques in long-range interacting physical systems to unlock new insights. Long-range interactions, where forces extend over large distances, are of particular interest, since they create unusual physical behaviours like fast information spread and long-lasting states. To describe these complex systems, we use mathematical tools like the functional renormalization group (fRG) and simulations on a grid (lattice models). These tools provide data, which can be analysed by machine learning models to better understand the relevant (...) dynamical components of the system. Furthermore, the data can be used to train ML models, like those used in language models (e.g., GPT), to emulate these interactions. By combining physics and ML, we hope to improve our understanding of such complex, multi-scale data and behaviours!
This EP investigates how we can use machine learning (ML) techniques in long-range interacting physical systems to unlock new insights. Long-range interactions, where forces extend over large distances, are of particular interest, since they create unusual physical behaviours like fast information spread and long-lasting states. To describe these complex systems, we use mathematical tools like the functional renormalization group (fRG) and simulations on a grid (lattice models). These tools provide data, which can be analysed by machine learning models to better understand the relevant (...) dynamical components of the system. Furthermore, the data can be used to train ML models, like those used in language models (e.g., GPT), to emulate these interactions. By combining physics and ML, we hope to improve our understanding of such complex, multi-scale data and behaviours!
53. Motion of Light Around Vectorized Black Holes
Jingqian Gou, Lavinia Heisenberg, Hui-Min Wang

Generalized Proca (GP) theories describe the interaction of vector fields with gravity, providing a framework for understanding phenomena such as black holes and cosmological evolution beyond the scope of traditional general relativity (GR). A central tenet of GR is the no-hair theorem, which asserts that black holes can be uniquely described by just three parameters: mass, charge, and angular momentum. This theorem implies that black holes cannot possess any additional fields, or “hair.” Any detection of such hair would represent a groundbreaking departure from GR. This project aims to investigate the motion of particles, including photons, around a rotating black hole with “hair” in the context of GP theories. While current studies of black hole solutions in GP theories have been limited to stationary, non-rotating black holes, our first goal is to develop new rotating black hole solutions in GP theories and analyse their deviations from the Kerr metric in GR. We will also investigate the shadow of the GP black hole, which is formed by photon trajectories in strong gravitational fields. Unlike the circular shadow of the non-rotating black hole, the shape of the rotating black hole shadow is elongated due to the dragging effect, and we will study how the photon geodesics are altered in this novel context.
Generalized Proca (GP) theories describe the interaction of vector fields with gravity, providing a framework for understanding phenomena such as black holes and cosmological evolution beyond the scope of traditional general relativity (GR). A central tenet of GR is the no-hair theorem, which asserts that black holes can be uniquely described by just three parameters: mass, charge, and angular momentum. This theorem implies that black holes cannot possess any additional fields, or “hair.” Any detection of such hair would represent a groundbreaking departure from GR. This project aims to (...) investigate the motion of particles, including photons, around a rotating black hole with “hair” in the context of GP theories. While current studies of black hole solutions in GP theories have been limited to stationary, non-rotating black holes, our first goal is to develop new rotating black hole solutions in GP theories and analyse their deviations from the Kerr metric in GR. We will also investigate the shadow of the GP black hole, which is formed by photon trajectories in strong gravitational fields. Unlike the circular shadow of the non-rotating black hole, the shape of the rotating black hole shadow is elongated due to the dragging effect, and we will study how the photon geodesics are altered in this novel context.
52. Resolving Spin Correlations in a Disordered Spin System
Valentina Salazar Silva, Selim Jochim, Matthias Weidemüller, et al.
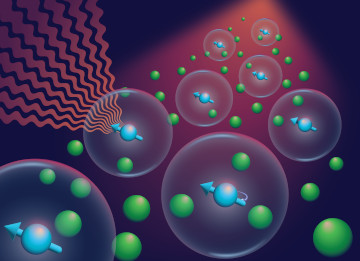
Rydberg systems are crucial tools in atomic physics due to their strong, long-range dipole-dipole interactions, which enable the investigation of fundamental properties of strong interacting matter, and advanced applications such as quantum simulation and quantum information processing. Mapping many-body spin systems onto tunable Rydberg states has allowed us to observe stretched relaxation dynamics in disordered spin systems on intermediate timescales, which is not captured by mean-field theory. Instead, the observed dynamics were modelled by considering interacting pairs of nearest neighbour spins, which points to an emergent integrability of the system. Until now, our diagnostics have focused on global quantities of disordered spin systems, like density and magnetization. The next step is to explore integrability at a microscopic level, studying local pair-correlations via fluorescence imaging. Our goal is to exploit the mapping of Rydberg states onto two different ground states that can be imaged subsequently to achieve state and single-atom resolution.
Rydberg systems are crucial tools in atomic physics due to their strong, long-range dipole-dipole interactions, which enable the investigation of fundamental properties of strong interacting matter, and advanced applications such as quantum simulation and quantum information processing. Mapping many-body spin systems onto tunable Rydberg states has allowed us to observe stretched relaxation dynamics in disordered spin systems on intermediate timescales, which is not captured by mean-field theory. Instead, the observed dynamics were modelled by considering interacting pairs of nearest neighbour (...) spins, which points to an emergent integrability of the system. Until now, our diagnostics have focused on global quantities of disordered spin systems, like density and magnetization. The next step is to explore integrability at a microscopic level, studying local pair-correlations via fluorescence imaging. Our goal is to exploit the mapping of Rydberg states onto two different ground states that can be imaged subsequently to achieve state and single-atom resolution.
51. Modelling Formation and Impact of the First Stars in the Universe
Ralf Klessen, Veronika Lipatova
The first stars built up from metal-free primordial gas at a time when the Universe was only a few hundred million years old, and it was originally proposed that they were solitary objects with masses much higher than what we observe in the Milky Way at present days. However, we know now that primordial star formation is subject to the same complexity as stellar birth today, and consequently, the first stars must have formed as members of hierarchical multiple stellar systems and across a wide range of masses. In this STRUCTURES project we address this complexity challenge by extending the A-SLOTH semi-analytic model, developed over the years here in Heidelberg, and employing it to study the formation of the first and second generations of stars within large representative cosmic volumes with unprecedented precision and predictive power. Our stochastic approach enables us to follow the formation and properties of millions of individual stars and binary systems for a wide range of galaxy formation prescriptions and different cosmological models, taking as input either data from numerical simulations of cosmic structure formation or from purely statistical calculations. We are in the process of incorporating improved stellar evolution models to address questions of the observability of the first galaxies with current and future Earth-bound and space-borne telescopes, and to investigate the metallicity evolution the early assembly history of the Milky Way and its satellite galaxies.
The first stars built up from metal-free primordial gas at a time when the Universe was only a few hundred million years old, and it was originally proposed that they were solitary objects with masses much higher than what we observe in the Milky Way at present days. However, we know now that primordial star formation is subject to the same complexity as stellar birth today, and consequently, the first stars must have formed as members of hierarchical multiple stellar systems and across a wide range of masses. In this STRUCTURES project we address this complexity challenge by extending the (...) A-SLOTH semi-analytic model, developed over the years here in Heidelberg, and employing it to study the formation of the first and second generations of stars within large representative cosmic volumes with unprecedented precision and predictive power. Our stochastic approach enables us to follow the formation and properties of millions of individual stars and binary systems for a wide range of galaxy formation prescriptions and different cosmological models, taking as input either data from numerical simulations of cosmic structure formation or from purely statistical calculations. We are in the process of incorporating improved stellar evolution models to address questions of the observability of the first galaxies with current and future Earth-bound and space-borne telescopes, and to investigate the metallicity evolution the early assembly history of the Milky Way and its satellite galaxies.
50. Mathematical Modelling and Model-based Data Analysis of Structured Stem Cell Systems
Carolin Lindow, Anna Marciniak-Czochra, Peter Bastian, in collaboration with Simon Anders, Ana Martin-Villalba, Piotr Gwiazda
In most animal organs, stem cell reservoirs are crucial for replenishing cells lost to injury or wear. Their fundamental functional property is stemness – the ability to self-renew and produce differentiated progeny. Current understanding suggests that stemness emerges from complex cell interactions in the niche, regulated by systemic feedbacks, rather than from individual cell programmes. How the resulting “perpetuation of stemness” is achieved is mechanistically unknown and an active research topic with potential translational implication in regenerative medicine and oncology. Recent progress in technology enabled the acquisition of high-resolution biological data that provided insights into their enormous heterogeneity. Analysing and interpreting this data requires new mathematical approaches, beyond traditional models like ordinary or partial differential equations, to account for both continuous and discrete transitions observed in single-cell data. Marciniak-Czochra and collaborators have proposed a novel framework using measure transport and dual problems, inspired by optimal transport theory, to model non-linear processes with growth and non-local interactions. The aim of this project is to develop models of stem cell population dynamics using measure differential equations to explore the role of heterogeneity in system control and robustness to perturbations.
In most animal organs, stem cell reservoirs are crucial for replenishing cells lost to injury or wear. Their fundamental functional property is stemness – the ability to self-renew and produce differentiated progeny. Current understanding suggests that stemness emerges from complex cell interactions in the niche, regulated by systemic feedbacks, rather than from individual cell programmes. How the resulting “perpetuation of stemness” is achieved is mechanistically unknown and an active research topic with potential translational implication in regenerative medicine and oncology. Recent (...) progress in technology enabled the acquisition of high-resolution biological data that provided insights into their enormous heterogeneity. Analysing and interpreting this data requires new mathematical approaches, beyond traditional models like ordinary or partial differential equations, to account for both continuous and discrete transitions observed in single-cell data. Marciniak-Czochra and collaborators have proposed a novel framework using measure transport and dual problems, inspired by optimal transport theory, to model non-linear processes with growth and non-local interactions. The aim of this project is to develop models of stem cell population dynamics using measure differential equations to explore the role of heterogeneity in system control and robustness to perturbations.
49. Learning Multi-Level Optimization on Statistical Manifolds
Stefania Petra, Roland Herzog, Christoph Schnörr, Yara Ayman Mohamed Fawzy Elshiaty
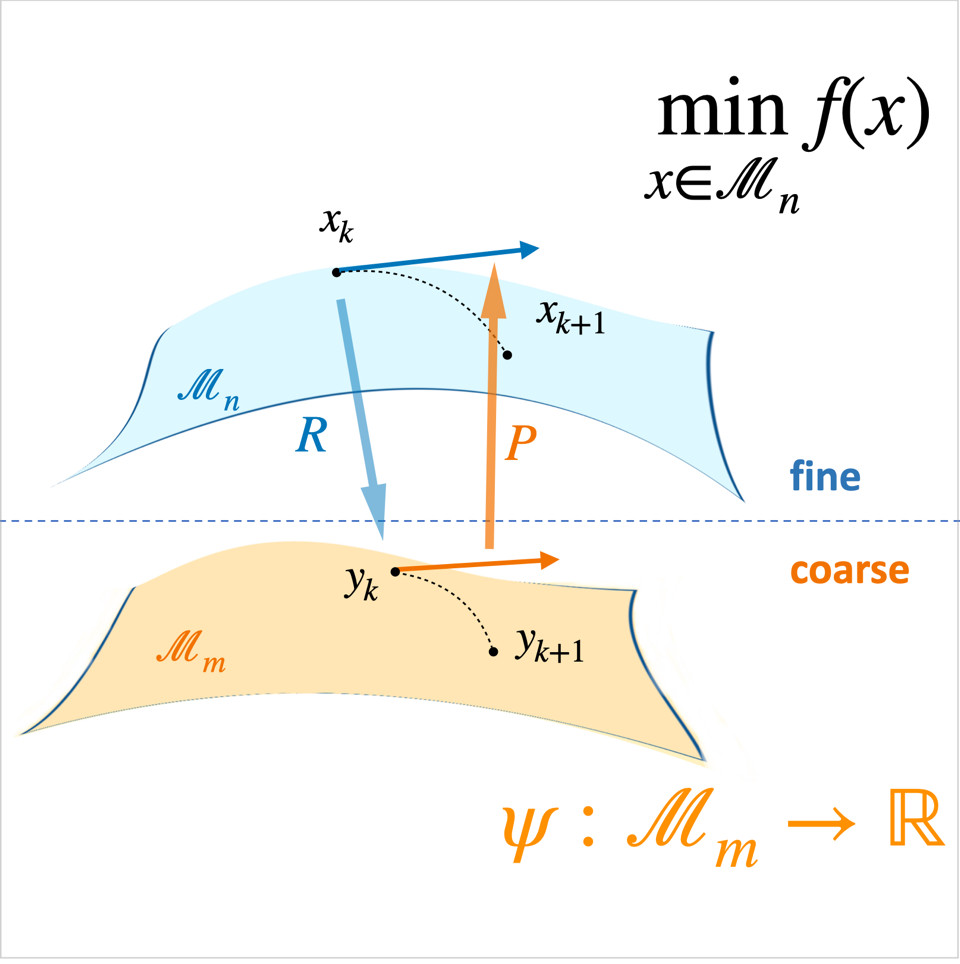
How can we efficiently solve large-scale optimization problems that have a hierarchical and geometric structure? This EP aims to accelerate the optimization of (non)convex problems using Riemannian multi-level techniques, which are well-established in classical multi-grid methods for solving PDEs but less explored in Riemannian optimization. We focus on representing high-dimensional problems on coarser levels for more efficient solutions. A key challenge is transferring quantities like iterates or descent directions between levels, which we address by learning problem-specific transfer operators. Additionally, we explore how these geometric transfer operators can faithfully approximate accelerated continuous Riemannian gradient flows. This EP also connects with CP6, machine learning, and data analysis, exploiting the synergy between geometry, multi-level representation, and machine learning.
How can we efficiently solve large-scale optimization problems that have a hierarchical and geometric structure? This EP aims to accelerate the optimization of (non)convex problems using Riemannian multi-level techniques, which are well-established in classical multi-grid methods for solving PDEs but less explored in Riemannian optimization. We focus on representing high-dimensional problems on coarser levels for more efficient solutions. A key challenge is transferring quantities like iterates or descent directions between levels, which we address by learning problem-specific transfer (...) operators. Additionally, we explore how these geometric transfer operators can faithfully approximate accelerated continuous Riemannian gradient flows. This EP also connects with CP6, machine learning, and data analysis, exploiting the synergy between geometry, multi-level representation, and machine learning.
48. Multi-Scale Spectral Generalized Finite Element Methods and Applications in the Modelling of Cell Motility
Zhongqian Wang, Robert Scheichl, Peter Bastian, Ulrich Schwarz
This project is dedicated to the fundamental development and analysis of novel multi-scale spectral generalized finite element methods (MS-GFEM) for complex biological and engineering structures. The main mathematical focus will be on extending MS-GFEM and its theoretical analysis from linear elasticity to non-linear problems, initially focusing on geometric non-linearities, but eventually also non-linear material properties. To enhance the efficiency of our algorithm in terms of selecting the number of eigenmodes, local grid size, local subdomain size, and other parameters, we will develop and analyse an offline-online goal-oriented adaptive (GOA) algorithm. We will focus on two main target applications: (i) carbon-fibre composite structures in aircraft design and (ii) cell mechanics due to dynamically created stress fibres. The analysis of MS-GFEM has already been developed for a wide-range of linear problems and we have successfully completed a first large-scale application of MS-GFEM to composite aero-structures. The project combines expertise and strengthens the link between researchers in functional analysis, numerical analysis, multi-scale simulation, high-performance scientific computing and biophysics. It is directly aligned with the activities in STRUCTURES' CP3 and the research efforts at Heidelberg University as a whole – including the strategy for time- and energy-efficient parallelization of PDE software in Hardware-Aware Scientific Computing, which is complimentary to STRUCTURES.
This project is dedicated to the fundamental development and analysis of novel multi-scale spectral generalized finite element methods (MS-GFEM) for complex biological and engineering structures. The main mathematical focus will be on extending MS-GFEM and its theoretical analysis from linear elasticity to non-linear problems, initially focusing on geometric non-linearities, but eventually also non-linear material properties. To enhance the efficiency of our algorithm in terms of selecting the number of eigenmodes, local grid size, local subdomain size, and other parameters, we will develop (...) and analyse an offline-online goal-oriented adaptive (GOA) algorithm. We will focus on two main target applications: (i) carbon-fibre composite structures in aircraft design and (ii) cell mechanics due to dynamically created stress fibres. The analysis of MS-GFEM has already been developed for a wide-range of linear problems and we have successfully completed a first large-scale application of MS-GFEM to composite aero-structures. The project combines expertise and strengthens the link between researchers in functional analysis, numerical analysis, multi-scale simulation, high-performance scientific computing and biophysics. It is directly aligned with the activities in STRUCTURES' CP3 and the research efforts at Heidelberg University as a whole – including the strategy for time- and energy-efficient parallelization of PDE software in Hardware-Aware Scientific Computing, which is complimentary to STRUCTURES.
47. Enhancing Superconductivity Using Bose-Einstein Condensates and Photons
Richard Schmidt, Ekaterina Vlasiuk
Superconductors are materials that can conduct electricity with zero resistance when cooled below a critical temperature. Predicting this critical temperature and understanding the fundamental limits on its value is a major challenge in condensed matter theory. In this project, we explore how the critical temperature of an already superconducting system can be enhanced by exposing it to interactions with additional particles, for instance with bosonic particles, like photons, phonons, and excitons, which can occupy the same quantum state. The goal is to understand and possibly modify the limits on the critical temperature, which are traditionally tied to the Debye energy in conventional superconductors. Theoretical methods, including diagrammatic resummation and functional renormalization group techniques, will help to understand how the interaction between the bosonic medium and the superconductor affects phenomena like Cooper pair formation and the overall critical temperature. This research is closely connected to the broader goals of the STRUCTURES Cluster, bridging condensed matter theory, cold atoms, and 2D materials, and it may open up new directions for both fundamental understanding and experimental material research.
Superconductors are materials that can conduct electricity with zero resistance when cooled below a critical temperature. Predicting this critical temperature and understanding the fundamental limits on its value is a major challenge in condensed matter theory. In this project, we explore how the critical temperature of an already superconducting system can be enhanced by exposing it to interactions with additional particles, for instance with bosonic particles, like photons, phonons, and excitons, which can occupy the same quantum state. The goal is to understand and possibly modify the (...) limits on the critical temperature, which are traditionally tied to the Debye energy in conventional superconductors. Theoretical methods, including diagrammatic resummation and functional renormalization group techniques, will help to understand how the interaction between the bosonic medium and the superconductor affects phenomena like Cooper pair formation and the overall critical temperature. This research is closely connected to the broader goals of the STRUCTURES Cluster, bridging condensed matter theory, cold atoms, and 2D materials, and it may open up new directions for both fundamental understanding and experimental material research.
46. Digital Twin Architecture for Applications in Global Health
Matthias Weidemüller, Anna-Katharina Nitschke

Digital Twins could enable a personalized, digital representation of patients and thus provide valuable decision support in health care. This EP is working toward applying a novel knowledge-informed Digital Twin architecture to prevent and diagnose pandemic diseases in public health. In particular, together with international partners from global health science, we focus on hypertension and diabetes, which are among the most significant and rapidly growing diseases in low- and middle-income countries with relatively scarce healthcare resources. The EP intends to extend the concepts of CP6 to help us explore behavioural, demographic, and biological structures in large-scale population data and identify risk factors and practical categorizations for tailored screening processes. In perspective, a refined Digital Twin architecture allows us to establish an interface that community members can use without expert advice.
Digital Twins could enable a personalized, digital representation of patients and thus provide valuable decision support in health care. This EP is working toward applying a novel knowledge-informed Digital Twin architecture to prevent and diagnose pandemic diseases in public health. In particular, together with international partners from global health science, we focus on hypertension and diabetes, which are among the most significant and rapidly growing diseases in low- and middle-income countries with relatively scarce healthcare resources. The EP intends to extend the concepts of CP6 to (...) help us explore behavioural, demographic, and biological structures in large-scale population data and identify risk factors and practical categorizations for tailored screening processes. In perspective, a refined Digital Twin architecture allows us to establish an interface that community members can use without expert advice.
Call Winter 2022/23
45. Tensor Field Theories as a Pathway to Strongly-Coupled Dynamics From First Principles
Jürgen Berges, Razvan Gurau, Thimo Preis
Asymptotic freedom, a key property of the theory of the strong interaction, is crucial for the fundamental understanding of nature through quantum field theories. This phenomenon describes how interaction strength varies with characteristic energy – getting weaker as particles come close together, leading to important effects like hadronic confinement. Conventional wisdom holds that non-Abelian gauge fields are essential for a renormalizable field theory to exhibit asymptotic freedom. In this project, we present a novel strongly interacting tensor quantum field theory in four space-time dimensions that displays asymptotic freedom: the O(N)3 model with an imaginary tetrahedral coupling in the limit of many field components. The analytical tractability of this model raises the tantalizing possibility of addressing questions raised by the rich phenomenology resulting from asymptotic freedom in the ultraviolet and a strongly-coupled sector in the infrared.
Asymptotic freedom, a key property of the theory of the strong interaction, is crucial for the fundamental understanding of nature through quantum field theories. This phenomenon describes how interaction strength varies with characteristic energy – getting weaker as particles come close together, leading to important effects like hadronic confinement. Conventional wisdom holds that non-Abelian gauge fields are essential for a renormalizable field theory to exhibit asymptotic freedom. In this project, we present a novel strongly interacting tensor quantum field theory in four space-time (...) dimensions that displays asymptotic freedom: the O(N)3 model with an imaginary tetrahedral coupling in the limit of many field components. The analytical tractability of this model raises the tantalizing possibility of addressing questions raised by the rich phenomenology resulting from asymptotic freedom in the ultraviolet and a strongly-coupled sector in the infrared.
44. Structures in Dipolar Quantum Gases – Fully Quantum Numerics Towards New Experimental Observables
Lauriane Chomaz, Thomas Gasenzer, Wyatt Kirkby
Ultracold bosonic quantum gases with dipolar interactions exhibit rich physics, including exotic phases such as superfluidity, quantum-stabilized droplets, and supersolidity. This EP investigates the structure formation, dynamics, and universal properties of these systems. The project focuses on the development of several computational tools. These include a stochastic-projected extended Gross-Pitaevskii equation (SPeGPE) solver - a method for modelling dilute Bose gases at finite temperatures, a variational quasi-2D code for modelling flattened dipolar condensates with reduced computational cost thereby allowing dynamical simulations of large scale systems, and a so-called Complex Langevin method - an exact quantum Monte Carlo approach that has proven successful in dealing with large ensembles of weakly interacting particles in regimes where beyond mean-field effects are important. Based on these different techniques, we shed new light on the static as well as the dynamical formation of structures in long-range interacting quantum systems.
Ultracold bosonic quantum gases with dipolar interactions exhibit rich physics, including exotic phases such as superfluidity, quantum-stabilized droplets, and supersolidity. This EP investigates the structure formation, dynamics, and universal properties of these systems. The project focuses on the development of several computational tools. These include a stochastic-projected extended Gross-Pitaevskii equation (SPeGPE) solver - a method for modelling dilute Bose gases at finite temperatures, a variational quasi-2D code for modelling flattened dipolar condensates with reduced computational (...) cost thereby allowing dynamical simulations of large scale systems, and a so-called Complex Langevin method - an exact quantum Monte Carlo approach that has proven successful in dealing with large ensembles of weakly interacting particles in regimes where beyond mean-field effects are important. Based on these different techniques, we shed new light on the static as well as the dynamical formation of structures in long-range interacting quantum systems.
43. Quantum State Steering in an Ultracold Many Body System
Selim Jochim, Matthias Weidemüller, Maciej Gałka, Tobias Hammel, Maximilian Kaiser
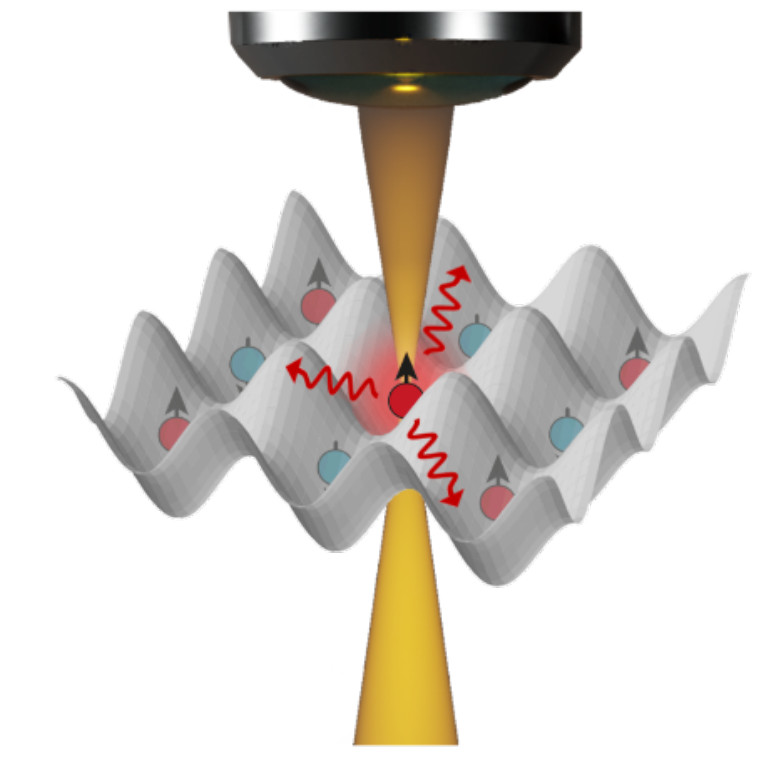
In the early stages of STRUCTURES, the Heidelberg Quantum Architecture (HQA) was established – a versatile platform for quantum-gas experiments characterized by high tunability, precision, modularity, and seamless project interoperability. This EP supports a key aspect of the HQA, focusing on an advanced technique for laser cooling and atom detection. Specifically, it targets the 2S→2P transition of lithium atoms at around 671 nm, manipulating it with an additional laser near the 2P→3S transition at around 813 nm to locally tune it in and out of resonance. This allows for optimizing the loading of cold atoms into optical traps. This technique, refined through machine learning, will be applicable to various atomic species, making it a valuable resource for multiple research groups within STRUCTURES.
In the early stages of STRUCTURES, the Heidelberg Quantum Architecture (HQA) was established – a versatile platform for quantum-gas experiments characterized by high tunability, precision, modularity, and seamless project interoperability. This EP supports a key aspect of the HQA, focusing on an advanced technique for laser cooling and atom detection. Specifically, it targets the 2S→2P transition of lithium atoms at around 671 nm, manipulating it with an additional laser near the 2P→3S transition at around 813 nm to locally tune it in and out of resonance. This allows for optimizing the (...) loading of cold atoms into optical traps. This technique, refined through machine learning, will be applicable to various atomic species, making it a valuable resource for multiple research groups within STRUCTURES.
42. Planet Formation Retrieval using Invertible Neural Networks
Victor Ksoll, Hubert Klahr, Thomas Henning, Remo Burn

Connecting observed planetary systems to their distinct formation process poses a challenge: while predicting observables from a global model of planet formation is straightforward, the inverse problem of estimating initial conditions and model parameters from observations is much more difficult. This EP addresses this by using invertible neural networks to infer the likely formation histories of observed planets, thereby bridging CP6 - Networks and Machine Learning with CP2 - Planet Formation. This approach transfers machine learning expertise to planetary sciences, offering a valuable tool for the exoplanet community. The project has already achieved notable results: we were able to explain the enigmatic gap in the size distribution of exoplanets around two Earth radii with the migration of icy sub-Neptunes into the inner regions of their planetary systems.
Connecting observed planetary systems to their distinct formation process poses a challenge: while predicting observables from a global model of planet formation is straightforward, the inverse problem of estimating initial conditions and model parameters from observations is much more difficult. This EP addresses this by using invertible neural networks to infer the likely formation histories of observed planets, thereby bridging CP6 - Networks and Machine Learning with CP2 - Planet Formation. This approach transfers machine learning expertise to planetary sciences, offering a valuable tool (...) for the exoplanet community. The project has already achieved notable results: we were able to explain the enigmatic gap in the size distribution of exoplanets around two Earth radii with the migration of icy sub-Neptunes into the inner regions of their planetary systems.
Call Summer 2022
41. Numerics and Visualization in the Three-Body Problem
Agustin Moreno, Peter Albers, Filip Sadlo

The aim of the EP is to investigate numerical aspects of the classical (circular, restricted) three-body problem (CR3BP), for the purposes of visualization and numerical study of closed orbits. Such problem concerns the motion of a massless particle in 3-space under the influence of two primaries which are assumed to move in circles. This is an old and outstanding open problem, for which we are trying to approach via numerical visualization. The basic idea, that goes back to work of Poincaré, is to take a section for the dynamics, i.e. a surface that intersects every orbit, and consider the associated return map, which associates to any point in the section the end point of the orbit after it comes back after a revolution. In good situations, i.e. the case where the Satellite moves in the plane, one can visualize this map via numerical methods, as shown in the figure. The goal of this EP is to do the same, but for the situation where it moves in 3-space, in which case the section is now 4-dimensional. This imposes certain difficulties, which are what makes the problem challenging and interesting.
The aim of the EP is to investigate numerical aspects of the classical (circular, restricted) three-body problem (CR3BP), for the purposes of visualization and numerical study of closed orbits. Such problem concerns the motion of a massless particle in 3-space under the influence of two primaries which are assumed to move in circles. This is an old and outstanding open problem, for which we are trying to approach via numerical visualization. The basic idea, that goes back to work of Poincaré, is to take a section for the dynamics, i.e. a surface that intersects every orbit, and consider the (...) associated return map, which associates to any point in the section the end point of the orbit after it comes back after a revolution. In good situations, i.e. the case where the Satellite moves in the plane, one can visualize this map via numerical methods, as shown in the figure. The goal of this EP is to do the same, but for the situation where it moves in 3-space, in which case the section is now 4-dimensional. This imposes certain difficulties, which are what makes the problem challenging and interesting.
40. Exploring Cosmic Structures through Gravitational Waves
Fabio D’Ambrosio, Lavinia Heisenberg, David Maibach

The recent measurement of gravitational waves heralds a new era in cosmology and astrophysics. In addition to insights gained through ongoing probes of the electromagnetic spectrum, such as radio telescopes and interferometers, we now have the ability to explore a variety of galactic and extragalactic gravitational wave sources. This breakthrough provides access to critical new information about the processes that shaped the universe as we observe it today, particularly regarding its large- and small-scale structures. This project seeks to employ both mathematical and data analysis techniques to investigate how resolved gravitational waves, along with the stochastic background from unresolved sources, can deepen our understanding of the physics governing the early and late universe.
The recent measurement of gravitational waves heralds a new era in cosmology and astrophysics. In addition to insights gained through ongoing probes of the electromagnetic spectrum, such as radio telescopes and interferometers, we now have the ability to explore a variety of galactic and extragalactic gravitational wave sources. This breakthrough provides access to critical new information about the processes that shaped the universe as we observe it today, particularly regarding its large- and small-scale structures. This project seeks to employ both mathematical and data analysis techniques (...) to investigate how resolved gravitational waves, along with the stochastic background from unresolved sources, can deepen our understanding of the physics governing the early and late universe.
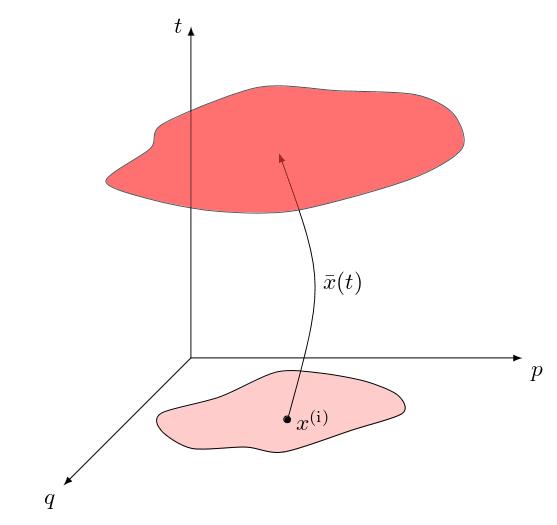
39. From Koopman-von Neumann to Structure Formation
Tristan Daus, Elena Kozlikin, Matthias Bartelmann, Thomas Gasenzer
How can we better understand complex classical systems where many particles interact and are out of equilibrium? This EP tackles this challenge with a novel approach inspired by the so-called Koopman-von Neumann formulation of classical mechanics. This new method allows to derive a detailed analytical propagator at the particle level and to develop a perturbation series based on classical particle interactions. The project has established both microscopic and macroscopic theories: the microscopic theory uses the Dyson series, while the macroscopic theory employs the Hubbard-Stratonovich transformation, familiar from statistical field theory in other areas. Additionally, the project has successfully linked this work to resummed kinetic field theory, a method used for describing cosmic structure formation – successfully reproducing and enhancing known results for the cosmic dark matter correlation function, while providing an intuitive understanding of the mechanisms driving structure growth.
How can we better understand complex classical systems where many particles interact and are out of equilibrium? This EP tackles this challenge with a novel approach inspired by the so-called Koopman-von Neumann formulation of classical mechanics. This new method allows to derive a detailed analytical propagator at the particle level and to develop a perturbation series based on classical particle interactions. The project has established both microscopic and macroscopic theories: the microscopic theory uses the Dyson series, while the macroscopic theory employs the Hubbard-Stratonovich (...) transformation, familiar from statistical field theory in other areas. Additionally, the project has successfully linked this work to resummed kinetic field theory, a method used for describing cosmic structure formation – successfully reproducing and enhancing known results for the cosmic dark matter correlation function, while providing an intuitive understanding of the mechanisms driving structure growth.
38. New Methods for Single Cell Data Analysis – a Promising Future Direction for STRUCTURES?
Fred Hamprecht, Anna Marciniak-Czochra, Anna Wienhard, Michael Bleher
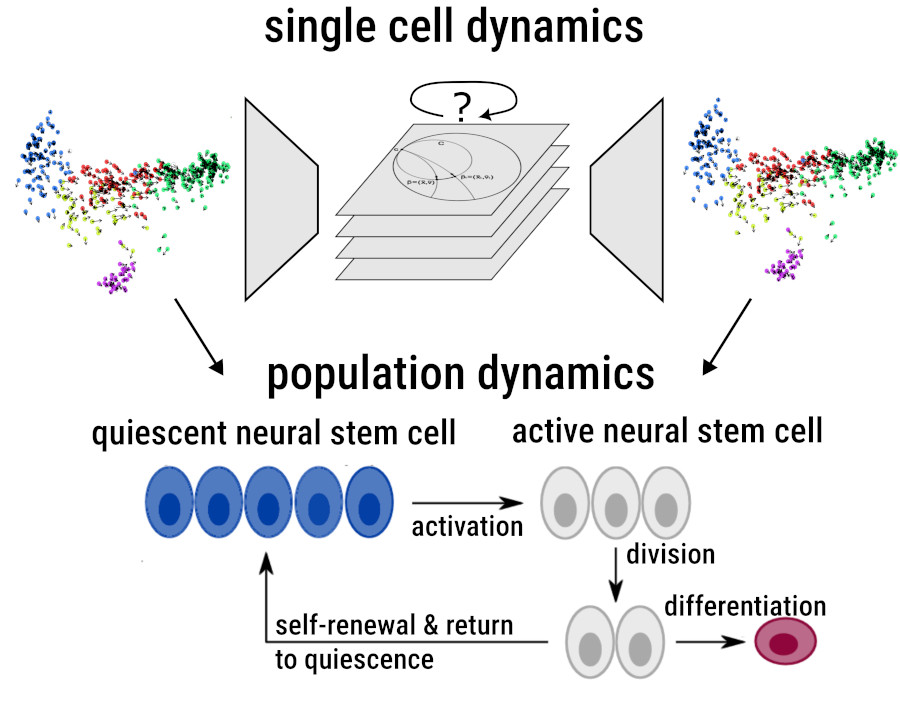
How can geometry improve the analysis of high-dimensional single cell gene expression data? This EP aims to accelerate the analysis of single cell data by taking a geometric perspective. Single cell technology, a breakthrough in biology, is generating data to answer new biological questions and improve our understanding of tissue development, regeneration, ageing and cancer development. This highly multi-dimensional data is rich in structure, which we aim to exploit for analysis of underlying processes. By combining mechanistic mathematical models (CP3), low-dimensional latent representations in machine learning (CP6), and dynamical systems on curved spaces (CP7), we aim to better understand single cell dynamics during differentiation. The EP is currently focusing on dynamic inference based on RNA velocity data represented on a tangent bundle of a Poincaré disk, using Hamiltonian dynamics of magnetic systems to model cellular processes during cell differentiation.
How can geometry improve the analysis of high-dimensional single cell gene expression data? This EP aims to accelerate the analysis of single cell data by taking a geometric perspective. Single cell technology, a breakthrough in biology, is generating data to answer new biological questions and improve our understanding of tissue development, regeneration, ageing and cancer development. This highly multi-dimensional data is rich in structure, which we aim to exploit for analysis of underlying processes. By combining mechanistic mathematical models (CP3), low-dimensional latent representations (...) in machine learning (CP6), and dynamical systems on curved spaces (CP7), we aim to better understand single cell dynamics during differentiation. The EP is currently focusing on dynamic inference based on RNA velocity data represented on a tangent bundle of a Poincaré disk, using Hamiltonian dynamics of magnetic systems to model cellular processes during cell differentiation.
37. Non-Circular Black Holes in Modified Gravity: Causal Structure and Thermodynamics
Timothy Anson, Lavinia Heisenberg, Carlos Pastor Marcos
In general relativity (GR), rotating black holes are described by the Kerr metric, which depends solely on the mass and spin of the object. A notable feature of Kerr black holes is their circularity, an isometry that links time-reflections to reflections in the azimuthal angle. This property simplifies the description of their spacetime and affects various aspects such as their event horizons and shadows. While black holes in GR are circular, non-circular black holes have been discovered in modified theories of gravity. By studying non-circular spacetimes, which are rarely explored, the project aims to uncover new insights into black hole dynamics, thermodynamics, and observable features like event horizons and geodesics. These investigations could reveal experimental differences from standard Kerr black holes, offering novel predictions for astrophysical observations and tests of alternative gravity theories.
In general relativity (GR), rotating black holes are described by the Kerr metric, which depends solely on the mass and spin of the object. A notable feature of Kerr black holes is their circularity, an isometry that links time-reflections to reflections in the azimuthal angle. This property simplifies the description of their spacetime and affects various aspects such as their event horizons and shadows. While black holes in GR are circular, non-circular black holes have been discovered in modified theories of gravity. By studying non-circular spacetimes, which are rarely explored, the (...) project aims to uncover new insights into black hole dynamics, thermodynamics, and observable features like event horizons and geodesics. These investigations could reveal experimental differences from standard Kerr black holes, offering novel predictions for astrophysical observations and tests of alternative gravity theories.
36. Hypothesis Testing in PDE Constrained Regression Problems
Jan Johannes, Anna Marciniak-Czochra, Maximilian Siebel
Scientific phenomena from biology or physics are often modelled using partial differential equations (PDE), but real-world data is typically affected by statistical noise, which needs to be properly accounted for. This project investigates non-parametric hypothesis testing for coefficient functions in PDE-constrained regression models, formalized as a Gaussian white noise model. This approach presents a multitude of challenges in functional analysis, probability theory, mathematical statistics and numerical analysis. The project extends the research envisioned in the cluster to link mathematical modelling using PDE (CP3) with statistical methods of data analysis (CP6).
Scientific phenomena from biology or physics are often modelled using partial differential equations (PDE), but real-world data is typically affected by statistical noise, which needs to be properly accounted for. This project investigates non-parametric hypothesis testing for coefficient functions in PDE-constrained regression models, formalized as a Gaussian white noise model. This approach presents a multitude of challenges in functional analysis, probability theory, mathematical statistics and numerical analysis. The project extends the research envisioned in the cluster to link (...) mathematical modelling using PDE (CP3) with statistical methods of data analysis (CP6).
35. Kinetic Field Theoretical Approach to Correlations in Active Matter Models
Carsten Littek, Falko Ziebert, Matthias Bartelmann
Self-propelled particles are the most studied realization of active matter, i.e. systems in out-of-equilibrium states that use energy sources or fluxes to move autonomously. As a collective, these particles can transition to flocking behaviour, similar to that observed in swarms of birds, moving cells, or bacteria. This phenomenon has been rationalized by the microscopic Vicsek model, which has been simulated and analysed using various mean-field approaches, as well as via the macroscopic Toner-Tu equations proposed on symmetry grounds, which all show discrepancies of the scaling exponents of correlation functions. The aim of this EP is to explore whether kinetic field theory (KFT) – an approach used to describe cosmic structure formation within CP1 and 2 – can be used to calculate the correlations from the microscopic interactions beyond first order and with well-defined truncation of perturbations. The EP aims to create a link between CP1, CP2 and CP3.
Self-propelled particles are the most studied realization of active matter, i.e. systems in out-of-equilibrium states that use energy sources or fluxes to move autonomously. As a collective, these particles can transition to flocking behaviour, similar to that observed in swarms of birds, moving cells, or bacteria. This phenomenon has been rationalized by the microscopic Vicsek model, which has been simulated and analysed using various mean-field approaches, as well as via the macroscopic Toner-Tu equations proposed on symmetry grounds, which all show discrepancies of the scaling exponents of (...) correlation functions. The aim of this EP is to explore whether kinetic field theory (KFT) – an approach used to describe cosmic structure formation within CP1 and 2 – can be used to calculate the correlations from the microscopic interactions beyond first order and with well-defined truncation of perturbations. The EP aims to create a link between CP1, CP2 and CP3.
34. Physical Interpretation of Optimization Stages in Neural Network Quantum States
Markus Oberthaler, Stefanie Czischek
Recent studies have shown that artificial neural networks (ANNs) can be used to model the behaviour of certain quantum systems, such as arrays of Rydberg atoms trapped in optical tweezers. During the process of learning the ground state, one can observe intriguing energy jumps, i.e. in few training steps the energy is significantly reduced. We are studying the hypothesis that these jumps are connected to the fact that the network spontaneously captures distant interactions in the system. Our first preliminary results confirm that the model quickly learns short-range patterns but needs more training to accurately represent longer-range correlation. Explaining this behaviour e.g. phase transitions, might help us to better understand how neural networks learn and improve their use in simulating quantum systems.
Recent studies have shown that artificial neural networks (ANNs) can be used to model the behaviour of certain quantum systems, such as arrays of Rydberg atoms trapped in optical tweezers. During the process of learning the ground state, one can observe intriguing energy jumps, i.e. in few training steps the energy is significantly reduced. We are studying the hypothesis that these jumps are connected to the fact that the network spontaneously captures distant interactions in the system. Our first preliminary results confirm that the model quickly learns short-range patterns but needs more (...) training to accurately represent longer-range correlation. Explaining this behaviour e.g. phase transitions, might help us to better understand how neural networks learn and improve their use in simulating quantum systems.
33. Band Structure Effects in 2D Materials and Ultracold Atoms
Xin Chen, Richard Schmidt
Band structures are crucial in condensed matter physics because they determine the electronic properties of materials, affecting their optical response and phenomena like superconductivity or magnetism. This EP takes a fresh approach by studying the role of band structure on a mobile quantum impurity problem. In this model, a single particle interacts with a group of fermions whose density can be adjusted. This interaction causes the single impurity particle to form a new state known as a Fermi polaron. This approach has several advantages: it is based on a well-defined model, provides a foundation for developing new many-body methods, can be experimentally realized in both cold atoms and atomically thin solid-state materials, and can help understand novel mechanisms for inducing superconductivity in 2D materials.
Band structures are crucial in condensed matter physics because they determine the electronic properties of materials, affecting their optical response and phenomena like superconductivity or magnetism. This EP takes a fresh approach by studying the role of band structure on a mobile quantum impurity problem. In this model, a single particle interacts with a group of fermions whose density can be adjusted. This interaction causes the single impurity particle to form a new state known as a Fermi polaron. This approach has several advantages: it is based on a well-defined model, provides a (...) foundation for developing new many-body methods, can be experimentally realized in both cold atoms and atomically thin solid-state materials, and can help understand novel mechanisms for inducing superconductivity in 2D materials.
32. Planckian Transport in Strongly Correlated Bosons
Félix Rose, Tilman Enss
This EP focused on the theoretical study of transport properties in quantum critical bosonic systems at finite temperatures. To achieve this, the so-called Local Potential Approximation (LPA) of the Functional Renormalization Group (FRG) was extended. Preliminary results included successful FRG-based computations of the critical classical 2D Ising model’s partial distribution function and identifying LPA shortcomings, which led to the adoption of a full potential Derivative Expansion (DE) scheme for more accurate results. This new approach promises more accurate results and will be used to further explore the transport properties of bosonic systems in various physical contexts.
This EP focused on the theoretical study of transport properties in quantum critical bosonic systems at finite temperatures. To achieve this, the so-called Local Potential Approximation (LPA) of the Functional Renormalization Group (FRG) was extended. Preliminary results included successful FRG-based computations of the critical classical 2D Ising model’s partial distribution function and identifying LPA shortcomings, which led to the adoption of a full potential Derivative Expansion (DE) scheme for more accurate results. This new approach promises more accurate results and will be used to (...) further explore the transport properties of bosonic systems in various physical contexts.
31. Physics-Informed Machine Learning for Quantum State Tomography
Martin Gärttner, Christoph Schnörr, Dmitrij Sitenko
Physics-informed machine learning defines an active research area in quantum science and technology. Key questions concern the parametrization of the machine learning component and the consistency of predicted output with physical laws. This project gathers corresponding expertise from quantum mechanics and from applied mathematics in order to develop novel tensor approximations for ground state computation of 2D-systems.
Call Winter 2021/22
30. Reconstructions of Potentials With Neural Differential Equations: Applications to Cosmic Inflation and Dark Energy
Björn Malte Schäfer, Lennart Röver
Understanding how fields in cosmology interact is crucial for advancing our understanding of fundamental physics theories. This EP explores the inference of interaction potentials on the basis of neural differential equations and physics-informed neural networks alongside advanced simulations. In both approaches, experimental errors are incorporated to construct suitable likelihoods for Bayesian inference, and it was discovered that so-called heteroscedastic loss functions in particular provide accurate descriptions of the total predictive error and are suitable optimization targets. The research, which focuses on dark energy and inflation, introduces a new analytical method for non-Gaussian statistical inference, replacing Monte-Carlo Markov-chain methods with canonical partition functions, aiming to advance analytical inference and to bridge conventional and neural methods, with physics-informed neural networks greatly accelerating the process.
Understanding how fields in cosmology interact is crucial for advancing our understanding of fundamental physics theories. This EP explores the inference of interaction potentials on the basis of neural differential equations and physics-informed neural networks alongside advanced simulations. In both approaches, experimental errors are incorporated to construct suitable likelihoods for Bayesian inference, and it was discovered that so-called heteroscedastic loss functions in particular provide accurate descriptions of the total predictive error and are suitable optimization targets. The (...) research, which focuses on dark energy and inflation, introduces a new analytical method for non-Gaussian statistical inference, replacing Monte-Carlo Markov-chain methods with canonical partition functions, aiming to advance analytical inference and to bridge conventional and neural methods, with physics-informed neural networks greatly accelerating the process.
29. Universality of Structure Formation from Gaussian Random Fields
Sara Konrad, Matthias Bartelmann, Manfred Salmhofer
This project aims to deepen our understanding of cosmic density fluctuations using kinetic field theory (KFT), a framework that analytically models the statistical behaviour of particle ensembles, both in and out of equilibrium. Previous work has shown that the evolved free density fluctuation power spectrum universally exhibits a k–3 slope at small scales, regardless of the cosmological model or type of dark matter. This slope is determined by the number of spatial dimensions and remains the same when particle interactions are introduced in a mean-field approximation. The only relevant assumptions are an initially Gaussian density-fluctuation field, that initial momentum fluctuations are correlated with density fluctuations by the continuity equation, and that certain moments of the initial power spectrum exist. Key outcomes of the EP include developing advanced computational tools for KFT, such as methods for solving highly oscillatory integrals, and revealing how initial conditions impact the asymptotic behaviour of power spectra. The project also explores how varying interaction laws influences structure growth. These findings shed light on universal patterns in cosmology and other particle systems. Methodically, the project connects CP1 and CP2, and potentially also studies of particle systems underlying symplectic dynamics.
This project aims to deepen our understanding of cosmic density fluctuations using kinetic field theory (KFT), a framework that analytically models the statistical behaviour of particle ensembles, both in and out of equilibrium. Previous work has shown that the evolved free density fluctuation power spectrum universally exhibits a k–3 slope at small scales, regardless of the cosmological model or type of dark matter. This slope is determined by the number of spatial dimensions and remains the same when particle interactions are introduced in a mean-field approximation. The only relevant (...) assumptions are an initially Gaussian density-fluctuation field, that initial momentum fluctuations are correlated with density fluctuations by the continuity equation, and that certain moments of the initial power spectrum exist. Key outcomes of the EP include developing advanced computational tools for KFT, such as methods for solving highly oscillatory integrals, and revealing how initial conditions impact the asymptotic behaviour of power spectra. The project also explores how varying interaction laws influences structure growth. These findings shed light on universal patterns in cosmology and other particle systems. Methodically, the project connects CP1 and CP2, and potentially also studies of particle systems underlying symplectic dynamics.
Call Summer 2021
28. Persistent Homology for Big Data
Freya Jensen, Guido Kanschat, Anna Wienhard
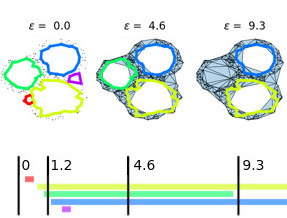
Topological data analysis, or more precisely persistent homology (PH), aims to find global structure in data. This global structure is described by connected components, holes and voids. Big data sets, such as those generated by astrophysical simulations, are difficult to analyse using existing PH-methods. The goal of this project is to develop a programme that can calculate PH for such large data sets mostly in parallel: We first divide the entire domain of the data set into smaller, overlapping subdomains and calculate their persistent homology. To glue the results together, we then calculate the corresponding Mayer-Vietoris spectral sequence. In return, we do not only get the PH of the complete dataset, but additional information such as local PH and the so called toroidal cycles for data sets with periodic boundary conditions.
Topological data analysis, or more precisely persistent homology (PH), aims to find global structure in data. This global structure is described by connected components, holes and voids. Big data sets, such as those generated by astrophysical simulations, are difficult to analyse using existing PH-methods. The goal of this project is to develop a programme that can calculate PH for such large data sets mostly in parallel: We first divide the entire domain of the data set into smaller, overlapping subdomains and calculate their persistent homology. To glue the results together, we then (...) calculate the corresponding Mayer-Vietoris spectral sequence. In return, we do not only get the PH of the complete dataset, but additional information such as local PH and the so called toroidal cycles for data sets with periodic boundary conditions.
27. Structure Formation in Driven Bose-Fermi Mixtures
Lauriane Chomaz, Matthias Weidemüller, Tilman Enss, Manfred Salmhofer, Michael Rautenberg
Ultracold atom experiments are one of the cleanest and most well-controlled implementations of many-body quantum systems. They are thus ideal for benchmarking theoretical models and discovering new phenomena. In such gases, impurities and defects are either absent or controllably introduced, and interatomic interactions can be tuned via Feshbach resonances. Using mixtures of two atomic species, a much broader range of few- and many-body effects can be studied, including mediated interactions and miscible/immiscible phases. Besides the study of equilibrium phenomena and states of matter, the cold-atom platform also provides exquisite access to out-of-equilibrium dynamics. Periodically driven mixture systems would provide access to rich physical effects such as spontaneous and mediated formation of structures, and interfacial dynamics. While a few experiments explored the Bose-Bose mixture case, the Bose-Fermi one remains untouched. In the latter case, the quantum nature of the system is expected to play a larger role due to Pauli pressure, behaving distinctly from classical fluids. In this EP, we conduct a joint theory-experiment investigation into the behaviour of quantum Fermi-Bose mixtures under (periodic) external driving in a broad range of regimes to shed new light on the formation of structures and correlations in quantum systems.
Ultracold atom experiments are one of the cleanest and most well-controlled implementations of many-body quantum systems. They are thus ideal for benchmarking theoretical models and discovering new phenomena. In such gases, impurities and defects are either absent or controllably introduced, and interatomic interactions can be tuned via Feshbach resonances. Using mixtures of two atomic species, a much broader range of few- and many-body effects can be studied, including mediated interactions and miscible/immiscible phases. Besides the study of equilibrium phenomena and states of matter, the (...) cold-atom platform also provides exquisite access to out-of-equilibrium dynamics. Periodically driven mixture systems would provide access to rich physical effects such as spontaneous and mediated formation of structures, and interfacial dynamics. While a few experiments explored the Bose-Bose mixture case, the Bose-Fermi one remains untouched. In the latter case, the quantum nature of the system is expected to play a larger role due to Pauli pressure, behaving distinctly from classical fluids. In this EP, we conduct a joint theory-experiment investigation into the behaviour of quantum Fermi-Bose mixtures under (periodic) external driving in a broad range of regimes to shed new light on the formation of structures and correlations in quantum systems.
26. Emergent Non-Equilibrium Phases in Driven Rydberg Systems
Martin Gärttner, Razvan Gurau
Quantum systems driven by a Hamiltonian that varies periodically in time are known as Floquet systems. Recent theoretical studies have predicted the emergence of meta-stable spatio-temporal structure including new phases of matter that are non-existent in undriven systems. Experiments with cold atoms excited to Rydberg states allow the implementation of a large class of such models. Numerical simulation, random matrix theory, and experimental realization are important assets that the STRUCTURES community lends to this EP. As understanding emergent dynamical phases in driven disordered Heisenberg spin models is realizable with Rydberg atoms, this EP can further devise experimental schemes for probing them. They employ numerical simulations and analytical tools to characterize Floquet phases of matter emerging in the Rydberg system under periodic driving, and propose experiments to verify those predictions in strongly interacting Floquet quantum matter. These objectives align well with the overall mission of STRUCTURES to understand how structure, collective phenomena, and complexity emerge from the fundamental laws of physics, and establish important links between experimental quantum dynamics and research lines of mathematical physics within our cluster.
Quantum systems driven by a Hamiltonian that varies periodically in time are known as Floquet systems. Recent theoretical studies have predicted the emergence of meta-stable spatio-temporal structure including new phases of matter that are non-existent in undriven systems. Experiments with cold atoms excited to Rydberg states allow the implementation of a large class of such models. Numerical simulation, random matrix theory, and experimental realization are important assets that the STRUCTURES community lends to this EP. As understanding emergent dynamical phases in driven disordered (...) Heisenberg spin models is realizable with Rydberg atoms, this EP can further devise experimental schemes for probing them. They employ numerical simulations and analytical tools to characterize Floquet phases of matter emerging in the Rydberg system under periodic driving, and propose experiments to verify those predictions in strongly interacting Floquet quantum matter. These objectives align well with the overall mission of STRUCTURES to understand how structure, collective phenomena, and complexity emerge from the fundamental laws of physics, and establish important links between experimental quantum dynamics and research lines of mathematical physics within our cluster.
25. Machine Learning in Density Functional Theory
Fred Hamprecht, Andreas Dreuw
Orbital-free density functional theory (OF-DFT) holds the promise to compute ground state
molecular properties at minimal cost. However, it has been held back by our inability to compute
the kinetic energy as a functional of the electron density only. Here, we set out to learn the
kinetic energy functional from ground truth provided by the more expensive Kohn-Sham density
functional theory. Such learning is confronted with two key challenges: Giving the model sufficient
expressivity and spatial context while limiting the memory footprint to afford computations on
a GPU; and creating a sufficiently broad distribution of training data to enable iterative density
optimization even when starting from a poor initial guess. In response, we introduce KineticNet,
an equivariant deep neural network architecture based on point convolutions adapted to the
prediction of quantities on molecular quadrature grids. From its methodological side, this project is well aligned with CP6 (“Networks and Machine Learning”), while the physical interpretation of a universal kinetic energy functional will draw on expertise from CP4 (“Quantum Structure and Dynamics”). Launched in 2021, this EP has evolved into a broader research focus within STRUCTURES, culminating in a new comprehensive project that will be titled CP µ (“Molecules: Conformational and electronic structure”).
Orbital-free density functional theory (OF-DFT) holds the promise to compute ground state
molecular properties at minimal cost. However, it has been held back by our inability to compute
the kinetic energy as a functional of the electron density only. Here, we set out to learn the
kinetic energy functional from ground truth provided by the more expensive Kohn-Sham density
functional theory. Such learning is confronted with two key challenges: Giving the model sufficient
expressivity and spatial context while limiting the memory footprint to afford computations on
a GPU; and creating a (...) sufficiently broad distribution of training data to enable iterative density
optimization even when starting from a poor initial guess. In response, we introduce KineticNet,
an equivariant deep neural network architecture based on point convolutions adapted to the
prediction of quantities on molecular quadrature grids. From its methodological side, this project is well aligned with CP6 (“Networks and Machine Learning”), while the physical interpretation of a universal kinetic energy functional will draw on expertise from CP4 (“Quantum Structure and Dynamics”). Launched in 2021, this EP has evolved into a broader research focus within STRUCTURES, culminating in a new comprehensive project that will be titled CP µ (“Molecules: Conformational and electronic structure”).
24. Critical Behaviour of Epidemic Models on Distinct Network Topologies and Applications to the Study of Brain Disease
Ana P. Millán, Nicolò Defenu, Tilman Enss
Epidemic processes describe the spread of a pathogen across a network. One application is to model information processing on brain networks to describe the progression of neurological diseases within the brain. Recent studies suggest that brain function may rely on mechanisms of criticality. The criticality hypothesis emphasizes the role physical phenomena, such as universality and scaling dynamics, may play in spreading processes in the brain. It is suggested that the phase transition between the non-contagion (disordered) and contagion (ordered) regimes of epidemic models is altered by the spectral dimension $d_s$, which characterizes the scaling of eigenvalues of the network Laplacian. Yet, critical scaling laws for inhomogeneous systems, such as complex networks, as well as the role of $d_s$, are still poorly understood. To acquire a better understanding of how disorder affects the universality of critical dynamics on a network, this EP first examines the synchronization and entrainment transitions of a nonequilibrium model and the phase transition of an equilibrium model, both on a one-dimensional long-range random ring network. This study develops a framework for linear theoretical analysis, and the results of the two models are compared with numerical simulations. Both theoretical and experimental studies are conducted on the effect of additional temporal heterogeneity in natural frequencies on synchronization. It is shown that in this case, disorder promotes synchronization.
Epidemic processes describe the spread of a pathogen across a network. One application is to model information processing on brain networks to describe the progression of neurological diseases within the brain. Recent studies suggest that brain function may rely on mechanisms of criticality. The criticality hypothesis emphasizes the role physical phenomena, such as universality and scaling dynamics, may play in spreading processes in the brain. It is suggested that the phase transition between the non-contagion (disordered) and contagion (ordered) regimes of epidemic models is altered by the (...) spectral dimension $d_s$, which characterizes the scaling of eigenvalues of the network Laplacian. Yet, critical scaling laws for inhomogeneous systems, such as complex networks, as well as the role of $d_s$, are still poorly understood. To acquire a better understanding of how disorder affects the universality of critical dynamics on a network, this EP first examines the synchronization and entrainment transitions of a nonequilibrium model and the phase transition of an equilibrium model, both on a one-dimensional long-range random ring network. This study develops a framework for linear theoretical analysis, and the results of the two models are compared with numerical simulations. Both theoretical and experimental studies are conducted on the effect of additional temporal heterogeneity in natural frequencies on synchronization. It is shown that in this case, disorder promotes synchronization.
Call Winter 2020/2021
23. The Semi-Random Method in the Continuous World
Felix Joos
You do not know which object you want to choose? Choose one at random! Potentially a bit surprisingly this is a common scenario in discrete mathematics. We do not know how to select a subset of a larger set with particular properties, however, a subset chosen uniformly at random among all subsets (of a certain size) does the job. This and more elaborated versions of this have had an enormous impact on discrete mathematics and have become known as the probabilistic method. In this exploratory project we have investigated how the probabilistic method can be applied to problems involving continuous spaces.
You do not know which object you want to choose? Choose one at random! Potentially a bit surprisingly this is a common scenario in discrete mathematics. We do not know how to select a subset of a larger set with particular properties, however, a subset chosen uniformly at random among all subsets (of a certain size) does the job. This and more elaborated versions of this have had an enormous impact on discrete mathematics and have become known as the probabilistic method. In this exploratory project we have investigated how the probabilistic method can be applied to problems involving (...) continuous spaces.
22. Machine Learning and the Renormalization Group
Lukas Kades, Ullrich Köthe, Jan M. Pawlowski, Manfred Salmhofer, Peter Sorrenson, Julian Urban, Jan Horak
Many aspects of how deep neural networks (DNNs) learn and distill information, particularly in image processing, closely resemble the systematic
removal of short-wavelength fluctuations within renormalisation group (RG) steps (Kadanoff block-spinnning). This entails similarities
of the dynamics and underlying structures within the two frameworks that can be observed from multiple perspectives. For instance, one can draw parallels
between feedforward layers and coarse-graining steps as part of a RG transformation. The training itself with an adaptation of the network weights as well as the propagation of data through the network can be identified as dynamical processes which can be easily mapped
into the RG framework. The latter represents a suitable tool to reduce the dimensionality and to uncover hidden patterns of the dynamics by its rigorous and
well-understood theoretical properties. We expect that unknown biases of a training problem can be narrowed down to a minimum by a clearly formulated training
objective in lattice field theory. In the present project we explore the RG-step interpretation in DNNs within the framework
of lattice field theory. This is done using both, predictive objectives such as classification and regression, as well as generative sampling.
In contrast to many real-world datasets, ensembles of field configurations from lattice simulations exhibit well-known properties as well
as tractable unnormalised probability weights. This provides a suitable environment for an investigation of scaling behaviour and performance of network architectures.
Developments done here have been taken further by the EP Long-Range Interaction and Machine Learning.
Many aspects of how deep neural networks (DNNs) learn and distill information, particularly in image processing, closely resemble the systematic
removal of short-wavelength fluctuations within renormalisation group (RG) steps (Kadanoff block-spinnning). This entails similarities
of the dynamics and underlying structures within the two frameworks that can be observed from multiple perspectives. For instance, one can draw parallels
between feedforward layers and coarse-graining steps as part of a RG transformation. The training itself with an adaptation of the network weights as well as the (...) propagation of data through the network can be identified as dynamical processes which can be easily mapped
into the RG framework. The latter represents a suitable tool to reduce the dimensionality and to uncover hidden patterns of the dynamics by its rigorous and
well-understood theoretical properties. We expect that unknown biases of a training problem can be narrowed down to a minimum by a clearly formulated training
objective in lattice field theory. In the present project we explore the RG-step interpretation in DNNs within the framework
of lattice field theory. This is done using both, predictive objectives such as classification and regression, as well as generative sampling.
In contrast to many real-world datasets, ensembles of field configurations from lattice simulations exhibit well-known properties as well
as tractable unnormalised probability weights. This provides a suitable environment for an investigation of scaling behaviour and performance of network architectures.
Developments done here have been taken further by the EP Long-Range Interaction and Machine Learning.
21. Opinion Dynamics and Kinetic Field Theory
Carsten Littek, Matthias Bartelmann
In cooperation with interdisciplinary research at the Heidelberg Academy of Sciences and Humanities, this project aims at applying methods from Kinetic Field Theory to systems in a linguistic context. Specifically, we are interested in decision making processes in communicative ensembles, i.e. how decisions are made and/or opinions are formed. Such opinion formations are strongly linked to phase transitions known from statistical physics, e.g. a consensus is equivalent to a magnetic phase.
To this end we work on a statistical field theory description of opinions – e.g. spins – on a complex network or carried by (possibly active) particles that can change by pairwise interactions with their neighbours and stochastic forces. This project strongly connects to the Comprehensive Projects CP1 (Cosmic Structure Formation) and CP2 (From Dust to Planets) by the application of statistical field theory. In addition, our endeavour is linked to CP6 (Networks and Machine Learning), since social communities typically form complex networks.
In cooperation with interdisciplinary research at the Heidelberg Academy of Sciences and Humanities, this project aims at applying methods from Kinetic Field Theory to systems in a linguistic context. Specifically, we are interested in decision making processes in communicative ensembles, i.e. how decisions are made and/or opinions are formed. Such opinion formations are strongly linked to phase transitions known from statistical physics, e.g. a consensus is equivalent to a magnetic phase.
To this end we work on a statistical field theory description of opinions – e.g. spins – on a complex (...) network or carried by (possibly active) particles that can change by pairwise interactions with their neighbours and stochastic forces. This project strongly connects to the Comprehensive Projects CP1 (Cosmic Structure Formation) and CP2 (From Dust to Planets) by the application of statistical field theory. In addition, our endeavour is linked to CP6 (Networks and Machine Learning), since social communities typically form complex networks.
20. Magnetic Field Structures from Dust Polarization – On the Alignment Dynamics of Interstellar Dust
Stefan Reissl, Ralf Klessen
Magnetic fields play a crucial role in structuring the matter involved in astrophysical processes on multiples scales from collapsing molecular clouds and star-formation up to the gaseous flows in galaxies. Studying and analysing the polarized light either emitted or absorbed by interstellar dust grain is one of the primary approaches to infer the structure and strength of magnetic fields in the Galaxy. However, the analysis of polarization data depends heavily on a quantitative understanding of the grain alignment physics itself. Interstellar dust grains are composed of different materials and come in a huge variety of complex fractal-like shapes. In this EP we have started to develop a self-consistent description of growth, spin-up and rotational fragmentation of interstellar grains and their alignment with respect to the magnetic field, the radiation field, as well as the relative flow between gas and dust. We conduct microkinetic simulations of dust formation and evolution and employ advanced radiative transfer methods to compute the detailed optical scatting properties. We average of large statistical ensembles in order to obtain effective cross sections and opacities for macroscopic models of the coupling between matter and radiation. In this project we cover an enormous range of scales, from micrometer-size dust grains to the Milky Way as a whole, and we bring together astrochemistry, microkinetic modelling, hydrodynamics and radiative transfer.
Magnetic fields play a crucial role in structuring the matter involved in astrophysical processes on multiples scales from collapsing molecular clouds and star-formation up to the gaseous flows in galaxies. Studying and analysing the polarized light either emitted or absorbed by interstellar dust grain is one of the primary approaches to infer the structure and strength of magnetic fields in the Galaxy. However, the analysis of polarization data depends heavily on a quantitative understanding of the grain alignment physics itself. Interstellar dust grains are composed of different materials (...) and come in a huge variety of complex fractal-like shapes. In this EP we have started to develop a self-consistent description of growth, spin-up and rotational fragmentation of interstellar grains and their alignment with respect to the magnetic field, the radiation field, as well as the relative flow between gas and dust. We conduct microkinetic simulations of dust formation and evolution and employ advanced radiative transfer methods to compute the detailed optical scatting properties. We average of large statistical ensembles in order to obtain effective cross sections and opacities for macroscopic models of the coupling between matter and radiation. In this project we cover an enormous range of scales, from micrometer-size dust grains to the Milky Way as a whole, and we bring together astrochemistry, microkinetic modelling, hydrodynamics and radiative transfer.
19. Small-Denominator Problems and Self-Reinforcing Singularities
Manfred Salmhofer, Kevin Paul Majowski
An important open renormalization problem in many-fermion physics is the full renormalization of the band function in systems with a Van Hove singularity (VHS). While renormalization of the Fermi velocity and the quasiparticle weight are well-understood, recent findings indicate that the Hessian may become singular – a phenomenon also suggested by experiments on cuprates and graphene. The aim of this project is to understand this specific class of systems, and to relate to the more general context of feedback loops that build up singularities, e.g. in self-organized criticality. Methodologically, we introduce a real-space regulator that avoids frequency and momentum cutoffs by restricting the propagator to a finite volume. This preserves important physical properties and the analyticity structure in complex frequency space. We applied this regulator to the two-loop self-consistency equation from the fermion model's Schwinger-Dyson equations, deriving a flow equation. Early results show that while the opening angle of the Fermi arcs approaches $\pi/2$ at the VHS, the second derivative does not converge, indicating a self-reinforcing singularity. Further work, including higher-order Taylor expansions, is needed to confirm this.
An important open renormalization problem in many-fermion physics is the full renormalization of the band function in systems with a Van Hove singularity (VHS). While renormalization of the Fermi velocity and the quasiparticle weight are well-understood, recent findings indicate that the Hessian may become singular – a phenomenon also suggested by experiments on cuprates and graphene. The aim of this project is to understand this specific class of systems, and to relate to the more general context of feedback loops that build up singularities, e.g. in self-organized criticality. (...) Methodologically, we introduce a real-space regulator that avoids frequency and momentum cutoffs by restricting the propagator to a finite volume. This preserves important physical properties and the analyticity structure in complex frequency space. We applied this regulator to the two-loop self-consistency equation from the fermion model's Schwinger-Dyson equations, deriving a flow equation. Early results show that while the opening angle of the Fermi arcs approaches $\pi/2$ at the VHS, the second derivative does not converge, indicating a self-reinforcing singularity. Further work, including higher-order Taylor expansions, is needed to confirm this.
18. Multilevel Monte Carlo for Lattice Field Theory
Robert Scheichl, Jürgen Berges, Yoshihito Kazashi
Monte Carlo simulations of strongly interacting quantum field theories such as Quantum Chromo Dynamics (QCD) on a space-time lattice predict fundamental physical observables from first principles and are crucial to interpret experimental results in particle physics. Traditional lattice simulations face challenges like critical slowdown and prohibitive costs near the so-called continuum limit, limiting precision in physical predictions. This project focuses on reducing the computational costs of lattice simulations with multilevel Monte Carlo methods. We explore hierarchical sampling as well as post-smoothing and Multigrid Monte Carlo (MGMC) approaches. This research promises to strengthen the synergy between quantum field theory research and advanced computational mathematics, aligning with the STRUCTURES Cluster's goals.
Monte Carlo simulations of strongly interacting quantum field theories such as Quantum Chromo Dynamics (QCD) on a space-time lattice predict fundamental physical observables from first principles and are crucial to interpret experimental results in particle physics. Traditional lattice simulations face challenges like critical slowdown and prohibitive costs near the so-called continuum limit, limiting precision in physical predictions. This project focuses on reducing the computational costs of lattice simulations with multilevel Monte Carlo methods. We explore hierarchical sampling as well as (...) post-smoothing and Multigrid Monte Carlo (MGMC) approaches. This research promises to strengthen the synergy between quantum field theory research and advanced computational mathematics, aligning with the STRUCTURES Cluster's goals.
17. Autocatalytic Reactions
Thomas Henning, Klaus Paschek
Self-sustaining and autocatalytic systems are thought to play a crucial role in the origins of life by driving the evolution of molecular complexity, structure formation, and genetic replication. Autocatalysis is a reaction where one or more of the reaction products act as a catalyst, creating positive feedback that allows for the spontaneous formation of more complex molecules. While autocatalytic reactions occur in a number of chemical systems, our fundamental understanding of this process remains limited despite significant theoretical advancements. A particular intriguing aspect of autocatalytic systems is their ability to produce order at the expense of the surrounding medium, a key feature in the transition from non-living to living matter. Additionally, these systems exhibit behaviours associated with life, such as information storage, self-organization, self-replication, and chemical evolution. This project investigates the emergence of molecular complexity by analysing the dynamics of chemical reaction networks undergoing autocatalysis using mathematical tools, including ordinary differential equations and stability analysis. Rather than studying complex RNA/DNA/protein-related systems or whole cells, we focus on simpler chemical systems that may serve as precursors to these complex systems. An example is the formose reaction, which synthesizes sugars – key building blocks of life – from formaldehyde and glycolaldehyde in an autocatalytic cycle. This approach allows us to generate a mathematical model that is applicable to real-world chemistry while remaining simple enough for broader generalization.
Self-sustaining and autocatalytic systems are thought to play a crucial role in the origins of life by driving the evolution of molecular complexity, structure formation, and genetic replication. Autocatalysis is a reaction where one or more of the reaction products act as a catalyst, creating positive feedback that allows for the spontaneous formation of more complex molecules. While autocatalytic reactions occur in a number of chemical systems, our fundamental understanding of this process remains limited despite significant theoretical advancements. A particular intriguing aspect of (...) autocatalytic systems is their ability to produce order at the expense of the surrounding medium, a key feature in the transition from non-living to living matter. Additionally, these systems exhibit behaviours associated with life, such as information storage, self-organization, self-replication, and chemical evolution. This project investigates the emergence of molecular complexity by analysing the dynamics of chemical reaction networks undergoing autocatalysis using mathematical tools, including ordinary differential equations and stability analysis. Rather than studying complex RNA/DNA/protein-related systems or whole cells, we focus on simpler chemical systems that may serve as precursors to these complex systems. An example is the formose reaction, which synthesizes sugars – key building blocks of life – from formaldehyde and glycolaldehyde in an autocatalytic cycle. This approach allows us to generate a mathematical model that is applicable to real-world chemistry while remaining simple enough for broader generalization.
16. A New Experimental Platform for Exploring Self-organization in Dipolar Quantum Gases
Lauriane Chomaz, Shuwei Jin

Ultracold quantum gases realize one of the most fruitful platform to explore few- and many-body quantum phenomena with an exquisite level of control and within pristine conditions. In this EP we design and build a new-generation experimental platform to produce quantum degenerate gases of highly magnetic atoms, which facilitate the study of long-range, anisotropic dipole-dipole interactions. The setup features compact design, high-resolution imaging, and versatile trapping schemes, allowing us to examine novel quantum effects, such as topologically driven ordering of both superfluid and solid natures, and push the boundaries of current understanding in dipolar systems. The successful experimental development of this EP has led to the recent EP "Structures in dipolar quantum gases - fully quantum numerics towards new experimental observables" as well as further contributions of the PI and her team to CP4 and CP5.
Ultracold quantum gases realize one of the most fruitful platform to explore few- and many-body quantum phenomena with an exquisite level of control and within pristine conditions. In this EP we design and build a new-generation experimental platform to produce quantum degenerate gases of highly magnetic atoms, which facilitate the study of long-range, anisotropic dipole-dipole interactions. The setup features compact design, high-resolution imaging, and versatile trapping schemes, allowing us to examine novel quantum effects, such as topologically driven ordering of both superfluid and solid (...) natures, and push the boundaries of current understanding in dipolar systems. The successful experimental development of this EP has led to the recent EP "Structures in dipolar quantum gases - fully quantum numerics towards new experimental observables" as well as further contributions of the PI and her team to CP4 and CP5.
Call Summer 2020
15. Subriemannian Billiards
Peter Albers, Lucas Dahinden, Beatrice Pozzetti
Subriemannian geometry studies motion in a constrained Riemannian manifold. The constraints arise by particular conditions, for example, the movement of a robotic arm must abide certain rules. In this sense, subriemannian geometry lends a tool to describe and predict the behaviour of constrained systems. Subriemannian billiards, as a particular branch of this field, is concerned with motion under billiard reflection laws. All geometrical properties of this branch can be explored and analysed. This EP deals with such an analysis, looking into geodesic flow, symmetry laws, contact distributions, the fibre bundle and singular points, to name a few questions. While they explore with particular interest the description of magnetic flow, there is a direct link to CP7 (“Quantum Geometry and Topological Methods in Physics: From Spectral Networks to Intersection Homology”) through the study of standard polygonal billiards, magnetic billiards, and symmetries with a large variety of methods. Collaboration with other STRUCTURES projects to visualize the subriemannian billiard flow is yet another important aim of this EP.
Subriemannian geometry studies motion in a constrained Riemannian manifold. The constraints arise by particular conditions, for example, the movement of a robotic arm must abide certain rules. In this sense, subriemannian geometry lends a tool to describe and predict the behaviour of constrained systems. Subriemannian billiards, as a particular branch of this field, is concerned with motion under billiard reflection laws. All geometrical properties of this branch can be explored and analysed. This EP deals with such an analysis, looking into geodesic flow, symmetry laws, contact distributions, (...) the fibre bundle and singular points, to name a few questions. While they explore with particular interest the description of magnetic flow, there is a direct link to CP7 (“Quantum Geometry and Topological Methods in Physics: From Spectral Networks to Intersection Homology”) through the study of standard polygonal billiards, magnetic billiards, and symmetries with a large variety of methods. Collaboration with other STRUCTURES projects to visualize the subriemannian billiard flow is yet another important aim of this EP.
14. Zero-Sum Evolutionary Games and Convex Hamiltonian Systems
Gabriele Benedetti, Davide Legacci
Evolutionary Game Theory is a well-established interdisciplinary subject with far-reaching applications to biology, physics of complex systems, social sciences and economics. It describes the evolution of a population of individuals divided into several subpopulations mutually interacting with each other. This EP focuses on applying differential geometry methods to model and predict such an evolution. More precisely, when all strategies of the evolutionary game perform the same on average (think for example of the rock-paper-scissors game), we use the underlying symplectic and Poisson geometry to detect the existence of periodic behaviours. This project shares research interests with the EP "Opinion Dynamics and Kinetic Field Theory", as both provide important insights into the evolution of a population and of complex systems, in general.
Evolutionary Game Theory is a well-established interdisciplinary subject with far-reaching applications to biology, physics of complex systems, social sciences and economics. It describes the evolution of a population of individuals divided into several subpopulations mutually interacting with each other. This EP focuses on applying differential geometry methods to model and predict such an evolution. More precisely, when all strategies of the evolutionary game perform the same on average (think for example of the rock-paper-scissors game), we use the underlying symplectic and Poisson geometry (...) to detect the existence of periodic behaviours. This project shares research interests with the EP "Opinion Dynamics and Kinetic Field Theory", as both provide important insights into the evolution of a population and of complex systems, in general.
13. Geometrical and Topological Characterization of State Spaces of High-dimensional Dynamical Systems Inferred From Empirical Data
Daniel Durstewitz, Filip Sadlo, Anna Wienhard, Zahra Monfared
For complex dynamical systems in physics, biology, or neuroscience, we usually do not know the governing equations. Often we may only have simplified (e.g., mean-field) models, the parameters of which are difficult to infer from data, and subject to the risk of model misspecification. In recent years, machine learning has provided data-driven alternatives for inferring data-generating mechanisms directly from observations. Recurrent neural networks (RNNs) have been successful for dynamical systems (DS), but often result in high-dimensional models (d > 10), making their analysis and comparison across different data sets challenging. This EP brings together expertise from various STRUCTURES groups and areas (machine learning, complex dynamical systems, geometric and topological (visual) analysis, neuroscience) to advance our understanding of DS inferred from data. The combination of these fields in this form is not yet existent and has a high innovative potential. The questions pursued are also of general relevance to any field dealing with (structure in) data generated by dynamical systems.
For complex dynamical systems in physics, biology, or neuroscience, we usually do not know the governing equations. Often we may only have simplified (e.g., mean-field) models, the parameters of which are difficult to infer from data, and subject to the risk of model misspecification. In recent years, machine learning has provided data-driven alternatives for inferring data-generating mechanisms directly from observations. Recurrent neural networks (RNNs) have been successful for dynamical systems (DS), but often result in high-dimensional models (d > 10), making their analysis and comparison (...) across different data sets challenging. This EP brings together expertise from various STRUCTURES groups and areas (machine learning, complex dynamical systems, geometric and topological (visual) analysis, neuroscience) to advance our understanding of DS inferred from data. The combination of these fields in this form is not yet existent and has a high innovative potential. The questions pursued are also of general relevance to any field dealing with (structure in) data generated by dynamical systems.
12. From the Fine-Structure Features of Stellar Haloes to the Assembly Histories of Their Galaxies
Annalisa Pillepich, Lukas Eisert

What can observations of galaxies tell us about their history? Galaxies evolve on timescales of millions to billions of years: this presents a significant challenge for their study, given that objects can be observed only at one specific time in cosmic history. To overcome this limitation, cosmological simulations are developed and used to study the evolution and interactions of thousands of galaxies in large, representative volumes of a model universe over cosmic time. Research in this EP has shown that it is in principle possible to infer the unobservable stellar assembly and merger histories of galaxies from their observable properties at any given point in time, by training machine learning models on the evolutionary histories of simulated galaxies. For this purpose, conditional invertible neural networks (cINN), also developed in Heidelberg, are used to model and understand the connections between observable and unobservable parameters in simulated data. Ultimately, and if the model galaxies are sufficiently realistic, these learnt connections can then be applied to real galaxy data.
What can observations of galaxies tell us about their history? Galaxies evolve on timescales of millions to billions of years: this presents a significant challenge for their study, given that objects can be observed only at one specific time in cosmic history. To overcome this limitation, cosmological simulations are developed and used to study the evolution and interactions of thousands of galaxies in large, representative volumes of a model universe over cosmic time. Research in this EP has shown that it is in principle possible to infer the unobservable stellar assembly and merger (...) histories of galaxies from their observable properties at any given point in time, by training machine learning models on the evolutionary histories of simulated galaxies. For this purpose, conditional invertible neural networks (cINN), also developed in Heidelberg, are used to model and understand the connections between observable and unobservable parameters in simulated data. Ultimately, and if the model galaxies are sufficiently realistic, these learnt connections can then be applied to real galaxy data.
11. “Singular Structures” in Models from Materials Science and Fluid Dynamics | Hysteresis, Interfaces and Non-Locality
Hans Knüpfer, Angkana Rüland, Ibrokhimbek Akramov
The formation of microstructures in macroscopic systems give rise to particular properties of the material or fluid in which they arise. The universality of the underlying principles by which these properties emerge is still a major open question. Some topics explored in this EP are the dynamics of microstructures in hysteresis, interfaces, fluids, elasticity, and long-range effects in ferromagnetic shape-memory alloys. The formation of microstructure and its interplay with physical constraints is investigated, with a focus on mesoscopic systems, described by partial differential equations. As in CP2, CP3, and CP4, the goal of this EP is to investigate the structure of solutions for complex, multiscale problems and their phase transitions. With the understanding of these structures, the design of functional materials is majorly benefited. All of the considered systems incorporate a multitude of materials as well as geometric length scales. The pattern formation in these systems is related to the presence of non-convexity, non-ellipticity and/or the presence of long-range interactions which may favour or suppress the development of microstructure.
The formation of microstructures in macroscopic systems give rise to particular properties of the material or fluid in which they arise. The universality of the underlying principles by which these properties emerge is still a major open question. Some topics explored in this EP are the dynamics of microstructures in hysteresis, interfaces, fluids, elasticity, and long-range effects in ferromagnetic shape-memory alloys. The formation of microstructure and its interplay with physical constraints is investigated, with a focus on mesoscopic systems, described by partial differential equations. As (...) in CP2, CP3, and CP4, the goal of this EP is to investigate the structure of solutions for complex, multiscale problems and their phase transitions. With the understanding of these structures, the design of functional materials is majorly benefited. All of the considered systems incorporate a multitude of materials as well as geometric length scales. The pattern formation in these systems is related to the presence of non-convexity, non-ellipticity and/or the presence of long-range interactions which may favour or suppress the development of microstructure.
Call Winter 2019/2020
10. Can Geometric Hydrodynamics Meet Dynamical Data Analysis?
Peter Albers, Christoph Schnörr, Fabrizio Savarino
Deep networks are omnipresent in many disciplines due to their unprecedented predictive power and the availability of software for training. Geometric hydrodynamics provides a powerful mathematical tool to encompass a plethora of natural phenomena. In this EP, research of dynamical data classification and symplectic geometry meet in a most surprising fashion. The project leverages expertise from pure mathematics (symplectic geometry, dynamical systems) and applied mathematics (machine learning, information geometry) in order to study mathematical structures that enable controlled measure transport by dynamical systems and corresponding networks. As the mathematics of deep networks and dynamical systems are major topics of STRUCTURES' Comprehensive Projects CP6 (“Networks and Machine Learning: Mathematical Structures”) and CP7 (“Quantum Geometry and Topological Methods in Physics: From Spectral Networks to Intersection Homology”), this EP feeds the mission of STRUCTURES in a relevant way: establishing such links within the cluster is of paramount importance to our collaboration.
Deep networks are omnipresent in many disciplines due to their unprecedented predictive power and the availability of software for training. Geometric hydrodynamics provides a powerful mathematical tool to encompass a plethora of natural phenomena. In this EP, research of dynamical data classification and symplectic geometry meet in a most surprising fashion. The project leverages expertise from pure mathematics (symplectic geometry, dynamical systems) and applied mathematics (machine learning, information geometry) in order to study mathematical structures that enable controlled measure (...) transport by dynamical systems and corresponding networks. As the mathematics of deep networks and dynamical systems are major topics of STRUCTURES' Comprehensive Projects CP6 (“Networks and Machine Learning: Mathematical Structures”) and CP7 (“Quantum Geometry and Topological Methods in Physics: From Spectral Networks to Intersection Homology”), this EP feeds the mission of STRUCTURES in a relevant way: establishing such links within the cluster is of paramount importance to our collaboration.
9. Bayesian Parameter Estimation for Mathematical Models of Self-organization and Biological Pattern Formation
Anna Marciniak-Czochra, Robert Scheichl
The formation of complex spatial architectures through self-organized processes is fundamental to a wide range of biological processes, including embryogenesis and tissue regeneration. The governing biophysical mechanisms have been the subject of experimental and theoretical research for several decades, yet in many cases remain poorly understood. Mathematical models have been demonstrated to be a valuable tool for investigating pattern formation mechanisms. However, a significant challenge inherent to their application is the absence of efficient techniques for parameter identification and model selection. These methods must be capable of operating without access to time-dependent data and must be applicable to situations where only a limited amount of data is available, describing the final structure. This presents a significant challenge, as patterns with the same model parameters but small variations in initial values can exhibit considerable differences in location and shape, e.g. mixed-mode Turing patterns. This EP proposes a new way to solve this problem using a Bayesian approach based on Correlation Integral Likelihood, in which high-dimensional pattern data is mapped to a low-dimensional random vector that follows a multivariate Gaussian distribution. The new approach is being used to compare classical Turing-type models with new mechano-chemical models of pattern formation. This EP brings together STRUCTURES the research on partial differential equations modelling of pattern formation done in CP3 with methods of data analysis undertaken by CP6.
The formation of complex spatial architectures through self-organized processes is fundamental to a wide range of biological processes, including embryogenesis and tissue regeneration. The governing biophysical mechanisms have been the subject of experimental and theoretical research for several decades, yet in many cases remain poorly understood. Mathematical models have been demonstrated to be a valuable tool for investigating pattern formation mechanisms. However, a significant challenge inherent to their application is the absence of efficient techniques for parameter identification and (...) model selection. These methods must be capable of operating without access to time-dependent data and must be applicable to situations where only a limited amount of data is available, describing the final structure. This presents a significant challenge, as patterns with the same model parameters but small variations in initial values can exhibit considerable differences in location and shape, e.g. mixed-mode Turing patterns. This EP proposes a new way to solve this problem using a Bayesian approach based on Correlation Integral Likelihood, in which high-dimensional pattern data is mapped to a low-dimensional random vector that follows a multivariate Gaussian distribution. The new approach is being used to compare classical Turing-type models with new mechano-chemical models of pattern formation. This EP brings together STRUCTURES the research on partial differential equations modelling of pattern formation done in CP3 with methods of data analysis undertaken by CP6.
8. Universality on Network Structures from Quantum Dynamics to Big Data
Nicolò Defenu, Tilman Enss, Matthias Weidemüller, Giacomo Bighin
The landscape of the O(N) universality classes as a function of the
symmetry index N and the spatial dimension d is one of the most
studied structures of contemporary physics. Modern renormalization
group (RG) approaches have allowed to exhibit within a single elegant
framework all the qualitative features of the traditional picture for
critical phenomena. In particular, the study of universal behaviour
in fractional dimensions has recently triggered a large interest in
the physics community, providing a fascinating scenario for the
universal properties of O(N) field theories in real dimensions.
In this context, physicists aim to find a spectral dimension that can
describe critical phenomena such as spontaneous symmetry breaking on
inhomogeneous structures and complex networks. This EP addresses determining the existence of such a dimension and the universality of
the described behaviour. Their tests are implemented both from a
theoretical and experimental perspective. They benefit from the use
of Rydberg atoms, to realize XXZ spin models on inhomogeneous random
graphs and find universal quantum dynamics as the disorder strength
is varied (CP4 and CP5). In particular, they seek to draw the
complete landscape of universality classes at spectral dimension
lower than 2; clarify the influence of the spectral dimension on
equilibration and thermalisation; compute spin dynamics on
experimentally realized graph; and compare with recent and
forthcoming measurements in Rydberg gases.
The outcome of their research may be applied to the analysis of large
biophysical and general datasets (CP7), benefit machine learning
problems, and yield novel insight in learning dynamics (CP6).
The landscape of the O(N) universality classes as a function of the
symmetry index N and the spatial dimension d is one of the most
studied structures of contemporary physics. Modern renormalization
group (RG) approaches have allowed to exhibit within a single elegant
framework all the qualitative features of the traditional picture for
critical phenomena. In particular, the study of universal behaviour
in fractional dimensions has recently triggered a large interest in
the physics community, providing a fascinating scenario for the
universal properties of O(N) field theories in real (...) dimensions.
In this context, physicists aim to find a spectral dimension that can
describe critical phenomena such as spontaneous symmetry breaking on
inhomogeneous structures and complex networks. This EP addresses determining the existence of such a dimension and the universality of
the described behaviour. Their tests are implemented both from a
theoretical and experimental perspective. They benefit from the use
of Rydberg atoms, to realize XXZ spin models on inhomogeneous random
graphs and find universal quantum dynamics as the disorder strength
is varied (CP4 and CP5). In particular, they seek to draw the
complete landscape of universality classes at spectral dimension
lower than 2; clarify the influence of the spectral dimension on
equilibration and thermalisation; compute spin dynamics on
experimentally realized graph; and compare with recent and
forthcoming measurements in Rydberg gases.
The outcome of their research may be applied to the analysis of large
biophysical and general datasets (CP7), benefit machine learning
problems, and yield novel insight in learning dynamics (CP6).
Call Summer 2019
7. Dynamics
Peter Albers, Ralf Klessen, Anna Marciniak-Czochra, Beatrice Pozzetti, Filip Sadlo, Manfred Salmhofer, Johannes Walcher, Anna Wienhard, Ingmar Saberi
Dynamical systems ideas appear throughout the research in STRUCTURES, explicitly mentioned in CP5, 6, and 7, and as a concept in virtually all CPs, albeit with a wide array of meaning. This EP establishes a forum where various concepts, incarnations, and theories of/on dynamical systems are discussed, exchanged, and investigated. In this way this EP seeks to familiarise STRUCTURES members with common threads of research mainly through a lectures series. This series covers topics such as astrodynamics, dynamics in the lab, quantum dynamics, dynamics in neural networks, dynamics in visualisation, and dynamics in mathematics. In time, this EP helped to initiate the EPs “Can geometric hydrodynamics meet dynamical data analysis?”, ”Subriemannian billiards”, ”Zero-sum evolutionary games and convex Hamiltonian systems”, and ”Geometrical and topological characterisation of state spaces of high-dimensional dynamical systems inferred from empirical data”.
Dynamical systems ideas appear throughout the research in STRUCTURES, explicitly mentioned in CP5, 6, and 7, and as a concept in virtually all CPs, albeit with a wide array of meaning. This EP establishes a forum where various concepts, incarnations, and theories of/on dynamical systems are discussed, exchanged, and investigated. In this way this EP seeks to familiarise STRUCTURES members with common threads of research mainly through a lectures series. This series covers topics such as astrodynamics, dynamics in the lab, quantum dynamics, dynamics in neural networks, dynamics in (...) visualisation, and dynamics in mathematics. In time, this EP helped to initiate the EPs “Can geometric hydrodynamics meet dynamical data analysis?”, ”Subriemannian billiards”, ”Zero-sum evolutionary games and convex Hamiltonian systems”, and ”Geometrical and topological characterisation of state spaces of high-dimensional dynamical systems inferred from empirical data”.
6. From Nilpotence Varieties to Twisted Supergravity: Towards Holomorphic Holography
Ingmar Saberi, Johannes Walcher
Supersymmetry has been a driving force behind many developments at the interface of quantum theory and geometry in the past several decades. The key insight is that the cancellation between bosonic and fermionic degrees of freedom dramatically simplifies the evaluation of supersymmetric observables. In recent years, there has been a resurgence of mathematical interest in this twisting procedure. One of the motivations is to derive mathematical consequences of physical dualities, including in particular holographic duality, as rigorously as possible from the microscopic models.
The principal goal of this EP is a structural understanding of the pure spinor superfield technique for this purpose. Two key results include the calculation of the twists of the ten-dimensional type IIB gravity and the six-dimensional N=(2,0) multiplet.
These topics align with efforts pursued in CP7 "Quantum geometry and topological methods in physics" and have been further investigated in the EP "Homological algebra of supersymmetry: Locality, unitarity, duality"
Supersymmetry has been a driving force behind many developments at the interface of quantum theory and geometry in the past several decades. The key insight is that the cancellation between bosonic and fermionic degrees of freedom dramatically simplifies the evaluation of supersymmetric observables. In recent years, there has been a resurgence of mathematical interest in this twisting procedure. One of the motivations is to derive mathematical consequences of physical dualities, including in particular holographic duality, as rigorously as possible from the microscopic models.
The principal (...) goal of this EP is a structural understanding of the pure spinor superfield technique for this purpose. Two key results include the calculation of the twists of the ten-dimensional type IIB gravity and the six-dimensional N=(2,0) multiplet.
These topics align with efforts pursued in CP7 "Quantum geometry and topological methods in physics" and have been further investigated in the EP "Homological algebra of supersymmetry: Locality, unitarity, duality"
5. Extending KFT in Association With the WIN-college on Decisions by Collectives
Matthias Bartelmann, Carsten Littek
The project aims at generalising the methods of Kinetic Field Theory (KFT). The generalisations shall target the investigation of collective properties of ensembles in a linguistic as well as a biological context, which might be comparable to phase transitions known in statistical physics. The interdisciplinary aims are already being funded by the Heidelberg Academy of Sciences and Humanities within the framework of the WIN-College.
As ensembles in these disciplines are largely different from classical particles, this involves the formulation of appropriate state spaces and dynamics of those states such that the concepts of statistical field theories become applicable. Thus, this project strongly relates to and connects methods employed in the Comprehensive Projects CP1 and CP2 via the non-equilibrium field theoretic approach, and also to graphical models and complex networks that are investigated in CP6.
The project aims at generalising the methods of Kinetic Field Theory (KFT). The generalisations shall target the investigation of collective properties of ensembles in a linguistic as well as a biological context, which might be comparable to phase transitions known in statistical physics. The interdisciplinary aims are already being funded by the Heidelberg Academy of Sciences and Humanities within the framework of the WIN-College.
As ensembles in these disciplines are largely different from classical particles, this involves the formulation of appropriate state spaces and dynamics of those (...) states such that the concepts of statistical field theories become applicable. Thus, this project strongly relates to and connects methods employed in the Comprehensive Projects CP1 and CP2 via the non-equilibrium field theoretic approach, and also to graphical models and complex networks that are investigated in CP6.
4. Mathematics and Data
Anna Wienhard, Michael Bleher, Maximilian Schmahl, Daniel Spitz
The EP “Mathematics and Data” aims to provide a central point of contact for researchers
using topological and geometric methods in data analysis. Over the past four years, different activities were organized by a team of doctoral students to accomplish this.
The EP began with an introductory lecture series in summer 2019, which served as a
common ground for future directions and projects. Since the winter term 2019/20, a regular Journal Club has served as a primary meeting point for researchers at Heidelberg University and beyond – attracting participants from various European universities. The EP has also hosted workshops annually for an international audience, focusing on the intersection of mathematics and data. Participants primarily had backgrounds in biology, physics, and mathematics.
The EP “Mathematics and Data” aims to provide a central point of contact for researchers
using topological and geometric methods in data analysis. Over the past four years, different activities were organized by a team of doctoral students to accomplish this.
The EP began with an introductory lecture series in summer 2019, which served as a
common ground for future directions and projects. Since the winter term 2019/20, a regular Journal Club has served as a primary meeting point for researchers at Heidelberg University and beyond – attracting participants from various European (...) universities. The EP has also hosted workshops annually for an international audience, focusing on the intersection of mathematics and data. Participants primarily had backgrounds in biology, physics, and mathematics.
Projects that started with STRUCTURES
3. Machine Learning in Astrophysics: Analysis of Young Stars
Ralf Klessen, Ullrich Köthe, Carsten Rother
In the exploratory project on machine learning in astrophysics, we explore the application of advanced machine learning techniques to modern astronomy and astrophysics and further develop these techniques taking the specific complexity and peculiarities of astronomical observations and astrophysical simulations into account. We employ modern generative models, especially invertible neural networks which belong to the larger class of normalizing flow methods, to characterize the physical properties of stars and star clusters based on photometric and spectroscopic data from ground-based and space-borne telescopes. The advantage of this approach is that it gives us access to the full posterior distribution function, which is highly advantageous when studying multi-modal or degenerate problems as is often the case in astronomical data, or when investigating complex correlations between parameters. Within STRUCTURES, the project spans a bridge between CP1 and CP2 on one side and CP6 and CP7 on the other.
In the exploratory project on machine learning in astrophysics, we explore the application of advanced machine learning techniques to modern astronomy and astrophysics and further develop these techniques taking the specific complexity and peculiarities of astronomical observations and astrophysical simulations into account. We employ modern generative models, especially invertible neural networks which belong to the larger class of normalizing flow methods, to characterize the physical properties of stars and star clusters based on photometric and spectroscopic data from ground-based and (...) space-borne telescopes. The advantage of this approach is that it gives us access to the full posterior distribution function, which is highly advantageous when studying multi-modal or degenerate problems as is often the case in astronomical data, or when investigating complex correlations between parameters. Within STRUCTURES, the project spans a bridge between CP1 and CP2 on one side and CP6 and CP7 on the other.
2. Modelling Large Near-Fractal Pre-Planetary Dust Aggregates
Cornelis Dullemond, Guido Kanschat, Peter Bastian, Dieter Heermann, et al.
Planet formation begins with the aggregation of micron-sized cosmic dust particles, growing through collisions into self-similar, ultra-fluffy structures known as "superaggregates," which remain tenuous even at hundreds of meters in size. Direct modelling of these structures, which may contain up to 1020 monomers, is unfeasible, so researchers use a hierarchical, nested modelling approach. Each level in this hierarchy is simulated individually, leveraging the properties derived from the previous scale. Because existing finite element tools could not handle these structures, a new software package, HyperHDG, was developed. HyperHDG implements hybridized discontinuous Galerkin (HDG) methods on graphs and hypergraphs, allowing each structural element to be represented as a single geometric object bound weakly by forces in the HDG framework. As efficient multigrid solvers for such HDG methods were not available at the start of this project, these schemes were developed and analysed as part of the EP. The resulting approach provides a unique avenue for simulating planetesimal formation, with the potential for unprecedented insight into early-stage aggregate mechanics.
Planet formation begins with the aggregation of micron-sized cosmic dust particles, growing through collisions into self-similar, ultra-fluffy structures known as "superaggregates," which remain tenuous even at hundreds of meters in size. Direct modelling of these structures, which may contain up to 1020 monomers, is unfeasible, so researchers use a hierarchical, nested modelling approach. Each level in this hierarchy is simulated individually, leveraging the properties derived from the previous scale. Because existing finite element tools could not handle these structures, a new software (...) package, HyperHDG, was developed. HyperHDG implements hybridized discontinuous Galerkin (HDG) methods on graphs and hypergraphs, allowing each structural element to be represented as a single geometric object bound weakly by forces in the HDG framework. As efficient multigrid solvers for such HDG methods were not available at the start of this project, these schemes were developed and analysed as part of the EP. The resulting approach provides a unique avenue for simulating planetesimal formation, with the potential for unprecedented insight into early-stage aggregate mechanics.
1. String Landscape Dynamics
Arthur Hebecker, Manfred Salmhofer, Johannes Walcher
Superstring theory is one of the leading candidates for a theory of quantum gravity. While its fundamental structure is simple and unique, its set of solutions is huge. Each of these solutions, also known as "vacua", corresponds to a different 4-dimensional effective field theory. This landscape of "string vacua" is the subject of the present project. We focus on several key open questions: Does the landscape contain de Sitter vacua or at least quasi-de Sitter vacua, such as those presumably describing slow-roll cosmological inflation and the accelerated expansion that our Universe apparently experiences today? What is the cosmological dynamics of the landscape as a whole, i.e. how do the different vacua get populated during cosmological evolution? Finally, related to the previous question and to the enormous complexity of the landscape: How can we make predictions in the "multiverse" made up from all those different string vacua? This is also known as the measure problem and is presumably one of the hardest questions in quantum gravity.
Superstring theory is one of the leading candidates for a theory of quantum gravity. While its fundamental structure is simple and unique, its set of solutions is huge. Each of these solutions, also known as "vacua", corresponds to a different 4-dimensional effective field theory. This landscape of "string vacua" is the subject of the present project. We focus on several key open questions: Does the landscape contain de Sitter vacua or at least quasi-de Sitter vacua, such as those presumably describing slow-roll cosmological inflation and the accelerated expansion that our Universe apparently (...) experiences today? What is the cosmological dynamics of the landscape as a whole, i.e. how do the different vacua get populated during cosmological evolution? Finally, related to the previous question and to the enormous complexity of the landscape: How can we make predictions in the "multiverse" made up from all those different string vacua? This is also known as the measure problem and is presumably one of the hardest questions in quantum gravity.
