Triangles with integer side lengths

Triangles are probably the simplest geometric objects in the two dimensional world. Draw three lines, hope they are not parallel (or go all through one point), and you end up with a structure which has so many intriguing properties that it is impossible to count them all. From congruence (which is comparing triangles as geometric objects) to trigonometry (which is comparing the intrinsic values such as angles and side lengths) and the list goes on and on.

The most famous formula related to triangles is without a doubt the Pythagorean Theorem: given a right triangle, we find that $a^2 + b^2 = c^2$, where $c$ is the longest side (called the hypotenuse, located opposite of the right angle). This equation is beautiful and in fact has integer solutions, for example $3^2 + 4^2 = 5^2$ or $5^2 + 12^2 = 13^2$. These are known as Pythagorean triples. Basically, the Pythagorean Theorem gives you a criterion for the existence of a triangle with integer side lengths, if you have a triple of integers. But of course, this is not a necessary condition. Pick for instance the equilateral triangle with side lengths of $1$. Although having integer side lengths, this triple does not satisfy the Pythagorean identity. So we can ask ourselves: can we find a necessary criterion for a triple of integers, such that it makes up a triangle? Can we construct a triangle with a given angle, such that all sides have integer side length? In this blog post, we will try to answer these questions.

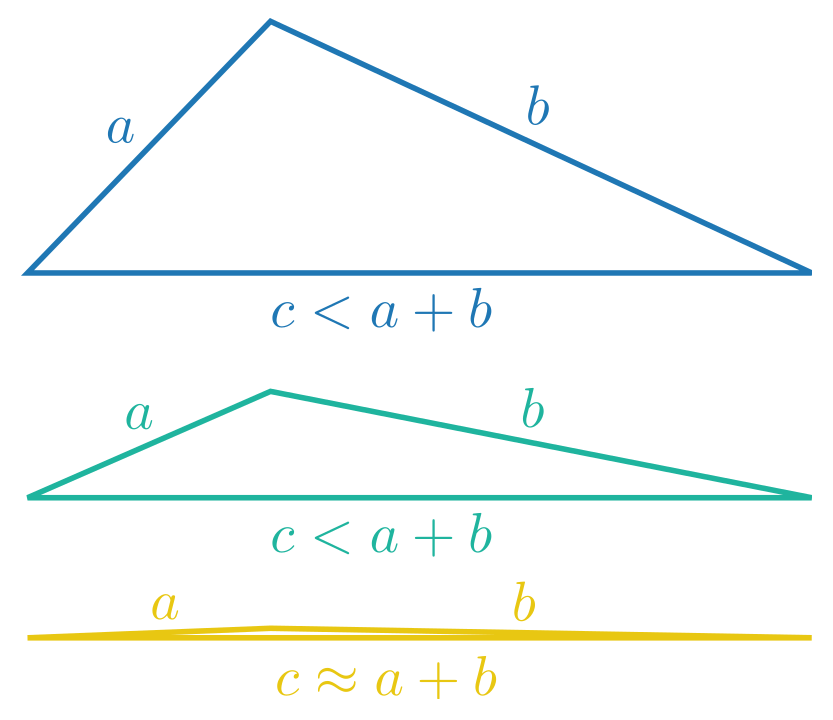
In order to have a chance to build a triangle with integer side lengths, the three corresponding numbers $a$, $b$, and $c$ have to fulfill $a + b \geq c$, $c$ being the longest side. This inequality is called the triangle inequality (for obvious reasons). To give an example that does not work, consider the triple $(1,1,3)$. It does not satisfy the triangle inequality and therefore, we cannot construct a triangle with these side lengths.

Another way to analyse this would be via the Cosine Theorem: given the angle $\theta$ opposite the longest side of the triangle, the Cosine Theorem states $c^2 = a^2 + b^2 – 2ab \, \cos(\theta)$. This may sound vaguely familiar to us and indeed, if $\theta = 90^\circ$, then $\cos(\theta) = 0$ and we end up with the famous Pythagorean Theorem. If $\theta = 60^\circ$, then $\cos(\theta) = ½$ and we arrive at $c^2 = a^2 + b^2 – ab$. One solution to this equation is given by $(1,1,1)$, the equilateral triangle.

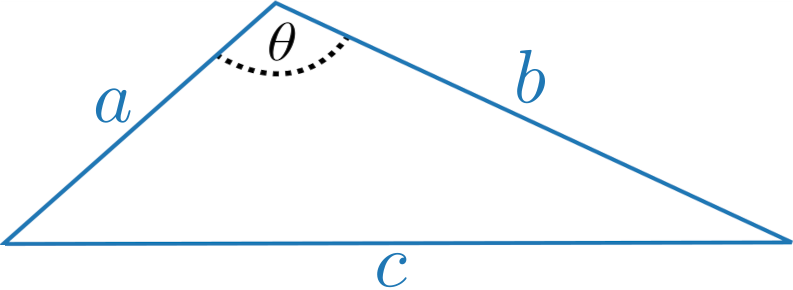
“But wait a minute!” an attentive reader might inject now. “any triple of integers satisfying the triangle inequality makes up a triangle. Just construct it with compass and ruler.” And this would be right! The construction of such triangles is basic and completely understood and our first question from above is hereby answered.

But what about constructability with a given angle? This is another matter. The three integer side lengths do not contain (a priori) information about the angles between them. Can we construct a triangle with integer side lengths for every angle that you are given (e.g. the angle opposite of the longest side). And the answer to that is: no. The reason for this is the Cosine Theorem: if $\cos(\theta)$ is irrational, the quantity $a^2 + b^2 – 2ab \, \cos(\theta)$ will be irrational as well, so $c^2$ is not an integer and therefore neither is $c$.

Things get interesting when we try to find integer solutions to the equation $c^2 = a^2 + b^2 – 2 ab \, \cos(\theta)$, and assume $\cos(\theta)$ to be rational. We can rewrite this equation as follows: define $x = a/c$, $y = b/c$ and $r = 2\cos(\theta)$, then $x^2 + y^2 – rxy = 1$. This is a Diophantine equation, a type of equation researched in number theory. This discipline exactly asks for the solvability of such equations in the field of rational numbers and this is related to the question that we are trying to answer.

In this case, it is not only possible to prove the existence of rational solutions, but we can even categorise all of them depending on the angle $\theta$. And the approach to the solution itself is pretty geometric as well. We first note that $-2 < r < 2$, and we can directly determine four solutions to this equation, which are all independent of $r$: $(1,0)$, $(-1,0)$, $(0,1)$ and $(0,-1)$. We also note that the solutions to this equation form an ellipse in the plane, which is tilted by $45^\circ$ to its side. Indeed, rotating the coordinates

$$\begin{align*}
x &= \hphantom{-} \cos(45^\circ) x’ + \sin(45^\circ) y’\\
y &= -\sin(45^\circ) x’ + \cos(45^\circ) y’ \end{align*} $$

results in

$$ \frac{(2 + r)}2 x^2 + \frac{(2 – r)}2 y^2 = 1,$$

which is an equation describing an ellipse.

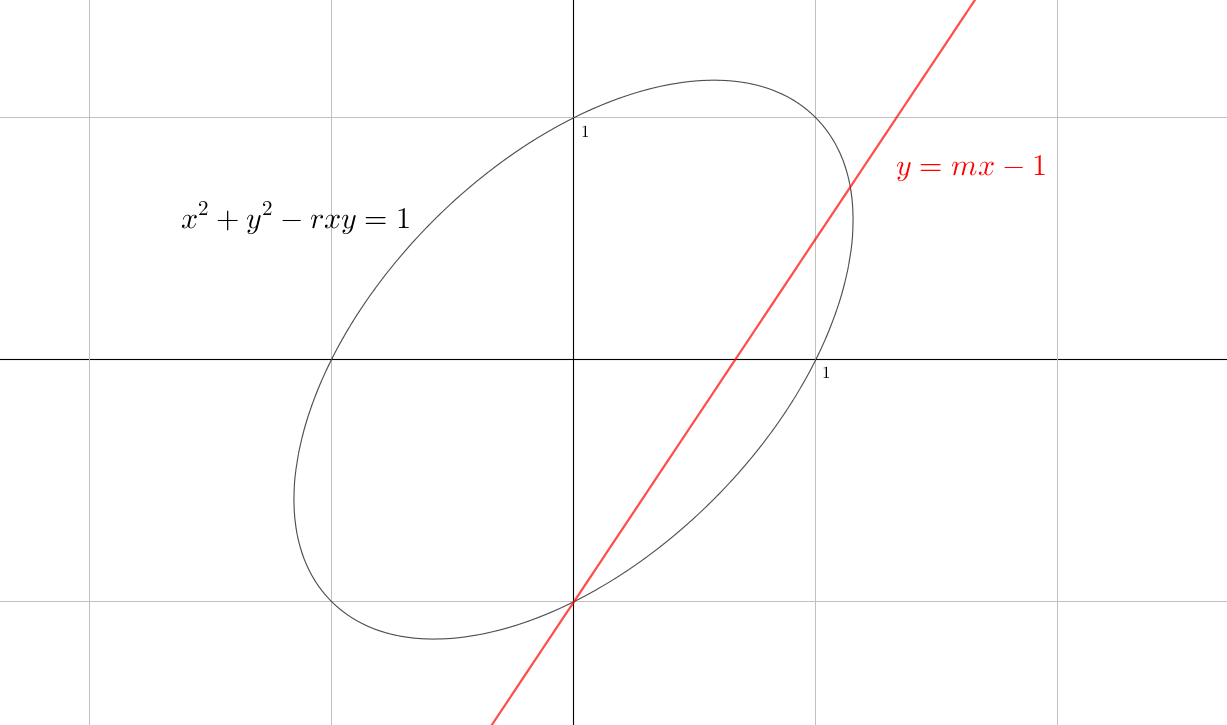
Now we need to intersect this ellipse with rational straight lines which will eventually give us all possible solutions. In fact we only need one straight line through $(-1,0)$ to obtain them. Let us look at $y = mx - 1$, where we choose $m = k/l$ to be a rational number. This is an equation for a straight line which intersects our ellipse in $(-1,0)$. To determine intersections with $x \neq 0$, we simply plug the equation for the straight line into the equation for our ellipse to obtain the non–trivial solutions

$$
\begin{align*}
x = \frac{2klq - l^2 p}{l^2 q + k^2q - kpl}, && y = \frac{k^2 q- l^2 q}{l^2 q + k^2q - kpl}, \quad (r = p/q)
\end{align*}
$$

which in turn implies

$$
\begin{align*}
a = 2klq - l^2p, && b = k^2 q - l^2 q, && c = l^2 q + k^2q - kpl.
\end{align*}
$$

This presents us with all of the possible solutions, which can be verified geometrically: we get every rational point on the ellipse. As with the Pythagorean triples, we have an infinite number of solutions which do not arise by scaling and the solutions can be characterised via the angle . But what is especially beautiful about all of this, is that we connected triangles with ellipses: every point with rational coordinates on the ellipse corresponds to a class of triangles with integer side lengths.