STRUCTURES Blog > Posts > Learning the Language of Time Series of Natural Phenomena
Learning the Language of Time Series of Natural Phenomena

Many real world applications repeatedly collect measurements of an object over time. Important examples are the price of a stock, sensor data in weather forecasting, and clinical measurements of patients monitored in intensive care units. The resulting data structure, called time series, can be described as ordered sets of real-valued variables, representing observations recorded sequentially over time. In this respect, time series data are similar to the way natural language is encoded for deep learning. This similarity has facilitated the successful application of state-of-the-art deep learning architectures developed for natural language processing (NLP) [7] to general time series forecasting (TSF). Given this initial success, the question arises as to how far the analogy between NLP and general time series goes? Can methods that exploit structural principles characterizing natural language also be fruitfully applied to time series? If so, we would be able to unveil the structure, or in accordance to NLP terminology, the language of a time series.
What makes natural language time series special are certain principles that have been proven useful in their analysis. One is the principle of the distributional structure of language [5] according to which “You shall know a word by the company it keeps!” [3]. This principle expresses the finding that words that are used and occur in the same contexts tend to purport similar meanings. Distributional structure is at the heart of neural language modeling, where a neural network is trained to predict the next word based on a sequence of preceding words [3]. The representations of words learned by a neural network during language modeling realize the distributional principle by assigning similar representation to words that appear in similar contexts. These so-called neural embeddings have proven to be useful not only to account for semantic aspects in many NLP tasks, but as a general technique to learn representations that account for similarity of inputs, and they are now an integral part of neural network modeling in general.
A second fundamental principle in NLP is compositionality. Compositionality describes the capacity of a language to generate an unbounded number of valid symbol sequences (sentences) based on only a finite set of elementary symbols (words). A simple, entirely data driven and yet general version of compositionality is given by the “Good-Enough Compositional Data Augmentation (GECA)” [1] method. This method defines a generative procedure for composing new sequences from a corpus by identifying sequence fragments that appear in similar contexts. The method is based on the distributional principle sketched above, where fragments that occur in the same context can be freely exchanged to yield another valid sequence. The simple composition rules it exploits can be applied to any kind of symbolic data. An exemplary application of GECA is presented below.
Good-Enough Compositional Data Augmentation (GECA)
| training data | M | A | N | B |
| She | picks | the suitcase | up | |
| M | C | N | D | |
| She | puts | the suitcase | down | |
| X | A | Y | B | |
| He | picks | the box | up | |
| augmentation | X | C | Y | D |
| He | puts | the box | down |
Data augmentation operation:
- Identify interchangeable (discontinuous) symbol sequences that appear in similar contexts in the training data, for example,
A…B andC…D appearing in contextM…N . - Find additional contexts in which interchangeable sequences appear, for example,
A…B in contextX…Y . - Augment the data with a synthesized training example by substituting interchangeable sequences into new contexts, for example, substitute
C…D intoX…Y .
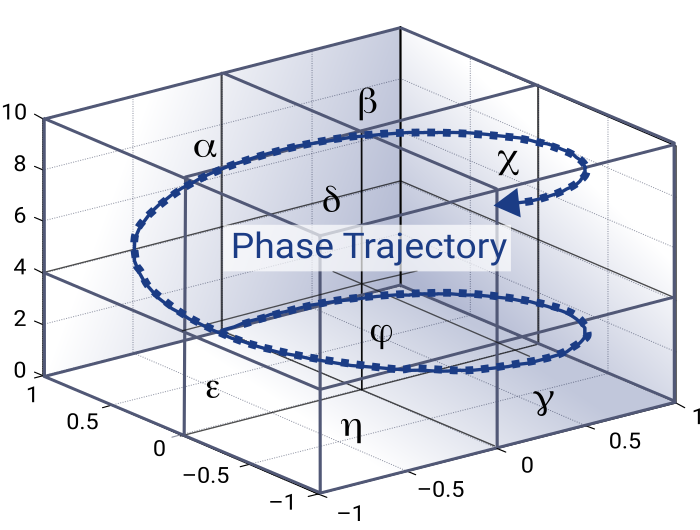
A prerequisite to applying GECA to general time series is an assignment of symbolic representations to trajectories of time series, i.e., we need to learn the vocabulary of time series, such as clinical measurements, before we can apply structural composition rules. In the traditional way to do this, one first partitions the multidimensional phase space spanned by the input variables of a time series into finitely many pieces. Then each partition is labeled by a specific symbol. A symbolic trajectory of a time series is obtained from the symbol sequence that corresponds to the successive partitions visited by the time series in its trajectory. An illustration of the trajectory of a time series through the phase space is given in Fig. 1.
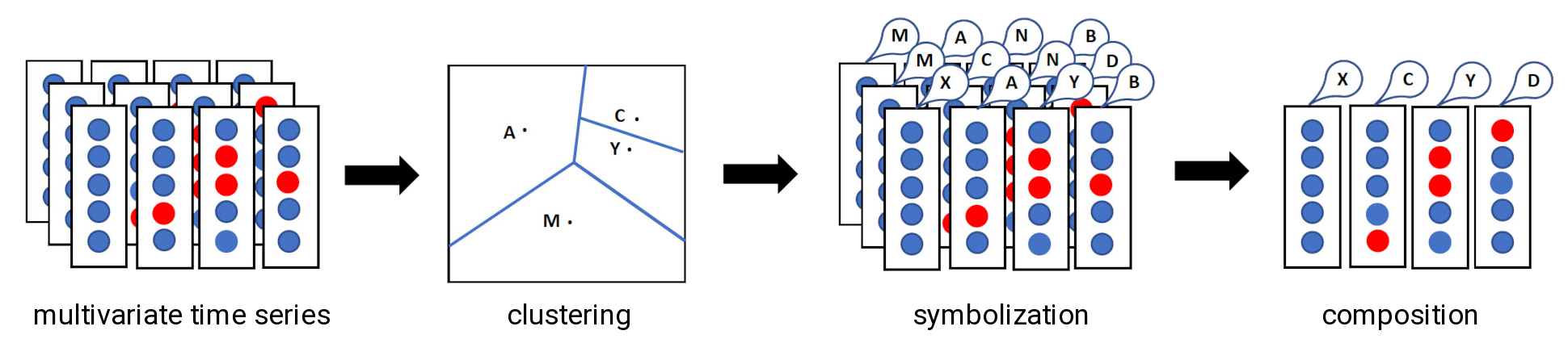
Since the number of possible symbol assignments grows exponentially with the number of input variables, the traditional approach is only feasible for very low dimensional time series. Instead of attempting to assign symbols directly, we start by creating neural embeddings of time series sub-fragments. After mapping the time series in the embedding space (whose dimensionality can be controlled) we apply clustering methods to partition this space. For example, by using the k-means clustering algorithm, we can create a symbolic representation of the time series whose computational learning cost is linear in the embedding dimension. An illustration of a possible experiment pipeline is given in Fig. 2. Starting from input data of multivariate clinical time series, we extract a real-valued vector representation from the hidden states of a so-called TSF Transformer model [6], which is then fed into a k-means clustering algorithm that allows us to assign a symbolic representation to time series clusters. Based on this vocabulary of symbolic representations, an entirely data-driven algorithm for compositional data augmentation [1] is applied to time series data, resulting in a set of rules that allows us to synthesize novel time series in a compositional manner.
But how can we assess whether or not the proposed system of symbolization and composition can actually generate valid “sentences” in the time series language? Once we have come up with a time series language, we can use it to compose new and previously unobserved synthetic time series. We can test the instrumental value of synthetic data by augmenting the training data of time series forecasting tasks, and see if the resulting model has an improved performance. If this is the case, we can say that we have learned a language that is able to generate, in this sense, meaningful time series.
To sum up, transferring methods for sequence-to-sequence learning from the area of NLP to TSF of natural phenomena has several benefits. First, the embeddings learned by neural networks allow us to identify similarities in time series, leading to an efficient approach to discretize time series in the natural world. This symbolic representation allows us to analyze patterns in time series, for example, we can detect similar clinical states that appear before the onset of particular syndromes in clinical time series. Last, applying compositional data augmentation to time series data allows us to enhance the training set of algorithms for various early prediction tasks. In ongoing work, we use the data augmentation capabilities of GECA to create synthetic training and test data for clinical time series forecasting that are on a par with original time series data and outperform randomization-based synthetic data on real-world clinical forecasting tasks.
References
- J. Andreas. Good-enough compositional data augmentation. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics (ACL), Online, 2020.
- Y. Bengio, R. Ducharme, P. Vincent, and C. Jauvin. A neural probabilistic language model. , 3:1137–1155, 2003.
- J. R. Firth. A synopsis of linguistic theory, 1930-55. In Studies in Linguistic Analysis, pages 1–31. Blackwell, 1957.
- S. Gupta and A. Ray. Symbolic dynamic filtering for data-driven pattern recognition. In E. A. Zoeller, editor, Pattern Recognition: Theory and Application, pages 17–71. Nova Science Publishers, 2007.
- Z. S. Harris. Distributional structure. , 10(2-3):146–162, 1954.
- M. Staniek, M. Fracarolli, M. Hagmann, and S. Riezler. Early prediction of causes (not effects) in healthcare by long-term clinical time series forecasting. , 252:1–29, 2024.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, L. Kaiser, and I. Polosukhin. Attention is all you need. In Advances in Neural Information Processing Systems (NIPS), Long Beach, CA, 2017.
Further Reading
Scientific Publication: Michael Hagmann, Michael Staniek, Stefan Riezler: “Compositionality in Time Series: A Proof of Concept using Symbolic Dynamics and Compositional Data Augmentation”. Transactions on Machine Learning Research. (2025)
Tags:
Machine Learning
Neural Networks
Time Series Forecasting
Computation