STRUCTURES Blog > Posts > What Do Herds of Animals Have In Common With Moving Magnets?
What Do Herds of Animals Have In Common With Moving Magnets?

A very familiar and yet fascinating sight is the collective and coherent motion of flocks of birds. Such collective behaviour is a rather ubiquitous phenomenon in nature and can be found across a variety of length scales: metres or even kilometres for animals (e.g. fish and wildebeests) or micrometres for bacteria. Seminal works by Tamás Vicsek et al. in 1995 and John Toner & Yuhai Tu in the same year led the way to understanding this phenomenon from a statistical physics and condensed matter physics point of view, which sparked interest in active matter systems.
Collective and coherent motion, oftentimes referred to as “flocking”, is a phenomenon regularly seen in systems consisting of many living organisms. These organisms may be as large as wildebeests moving through plains in Africa, flocks of birds in the sky, or as tiny as bacteria such as E. coli. Apart from these living systems, there are also artificial self-propelling particles (microswimmers), such as the class of Janus particles, that show flocking (Bechinger et al. 2016).
Translation Into Physics
The question is: what makes these birds or bacteria move in the same direction? There is no intelligent decision-making necessary, since even synthetic particles can exhibit such behaviour. Are there general principles that dictate the emergence of collective behaviour in systems of living organisms or synthetic particles? In order to answer these questions, we need to find out what properties these systems and their constituents share and if these properties are sufficient to explain the onset of collective motion starting from a random initial state of motion.
This translation into the framework of statistical physics was done by Tamás Vicsek and collaborators in a seminal work in 1995, which started the modern field of active matter. They devised a simple simulation scheme involving a large number of point-like particles in two dimensions to understand the phenomenon of flocking. The particles in the simulations were assumed to have a constant absolute velocity and, by interactions with their neighbours, their directions of motion could align. The collection of neighbours comprised all particles within a specified distance from a particle. In addition, the alignment was not perfect, i.e., a random angle was added to the aligned direction. This random perturbation is considered a natural consequence of both stochastic and deterministic factors affecting flocks (Vicsek & Zafeiris, 2012). This model is now generally referred to as the Vicsek model.
This particle-based model has several important properties that have consequences for the overall dynamics of the whole flock: the systems are far from thermodynamic equilibrium and their constituents are called active. This is a situation very different from, e.g., ideal gases – which are an idealized model concept often studied in physics, where particles obey Newtonian mechanics and both momentum and energy are conserved; resulting in the famous Maxwell-Boltzmann distribution of velocities. What do we mean by “active”? An active particle is able to convert energy from the environment into directed motion. In the case of living organisms, this may be energy gathered from food, and in synthetic particles, like Janus particles, a chemical reaction on their surface. The particles in the Vicsek model are self-propelled and move with a constant absolute velocity on a plane. By their activity, a collection of active particles makes up a non-equilibrium system since it does not conserve momentum. The only conserved quantity in this model is the number of particles.
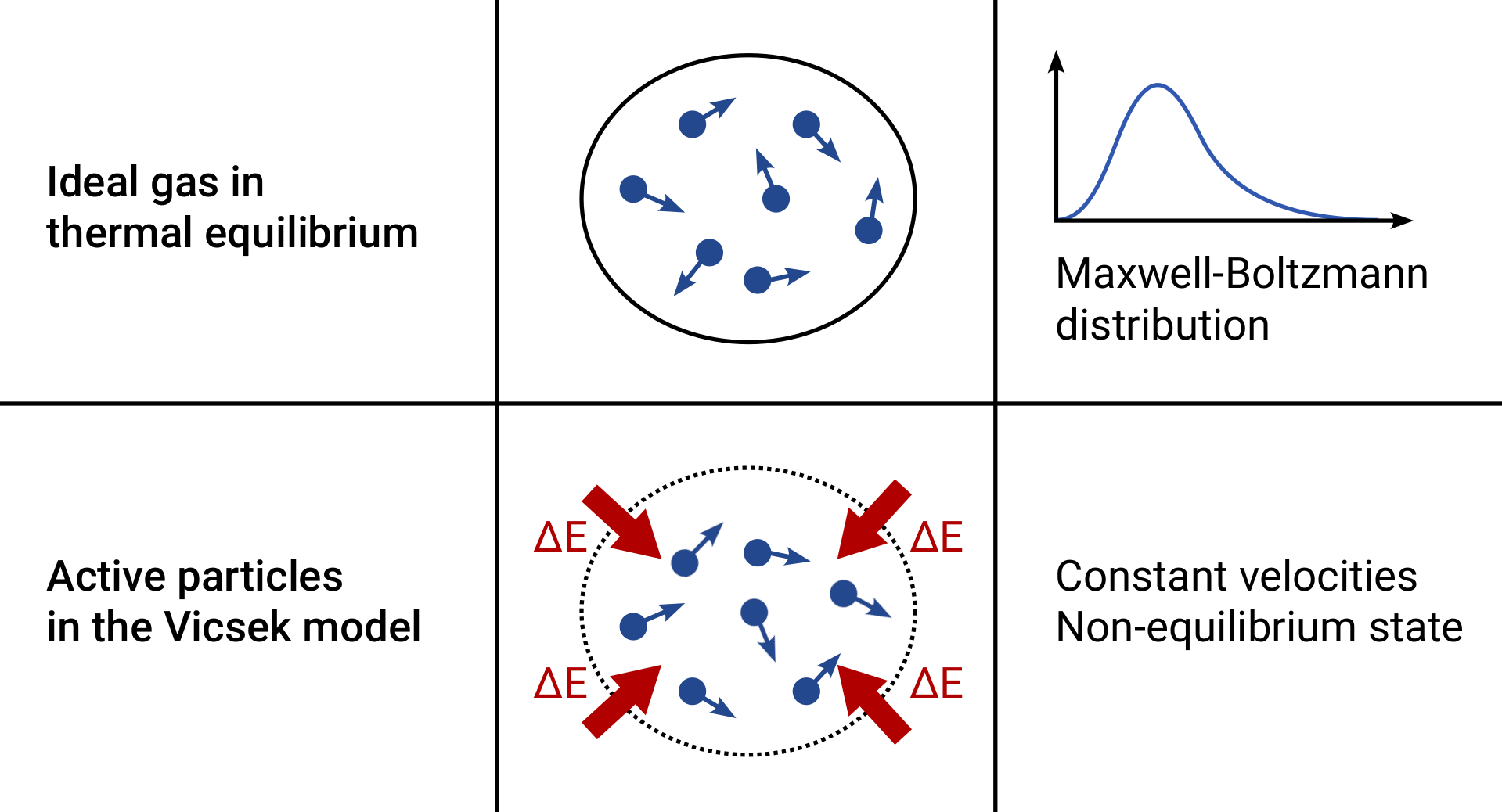
Another important property is that the system has a continuous symmetry, namely, it is rotationally symmetric. That means that no direction is preferred, and particles are equally likely to move in any direction. However, this system does not have one of the symmetries typical of classical mechanics: the Vicsek model is not Galilean invariant, which is directly related to the lack of momentum conservation. A physical system is Galilean invariant if the dynamics of that system are the same in all frames of reference that move relative to each other with constant velocity. In the Vicsek model, this is not true, since an observer moving at a constant speed relative to all self-propelled particles would measure a different velocity for every particle, depending on their direction of motion. Thus, the self-propelled particles are moving in a special reference frame, namely the one in which all particles have the same absolute velocity, albeit moving in different directions. The lack of Galilean invariance is particularly important in the formulation of hydrodynamic equations describing flocking, since it allows for more terms in the Navier-Stokes equation, which was pointed out by Toner & Tu in 1995.
Individual Active Particles
Before we go on to see how flocking can be achieved in systems of self-propelled particles, we want to see the difference in the motion of a single active particle compared to a single particle undergoing Brownian motion. In Fig. 2, taken from Bechinger et al. (2016), we show the trajectories of four particles with varying absolute velocities. Each particle can move with a velocity v in the direction given by the orientation angle φ on a two-dimensional plane. In addition, both the position and the orientation can change randomly by Brownian motion, which is usually the result of collisions of the particle with the molecules in the liquid it is suspended in. We see in Fig. 2 that for (b) v = 0, the two-dimensional motion is purely diffusive (i.e. driven entirely by random fluctuations) and independent of the direction angle φ. The mean position of the particles at any time is their starting point. But as soon as the particle is self-propelled with a velocity v > 0, its motion becomes a persistent random walk, i.e. the particle moves along the direction of its initial orientation for a finite persistence length before its direction is randomized. The persistence length increases with velocity.
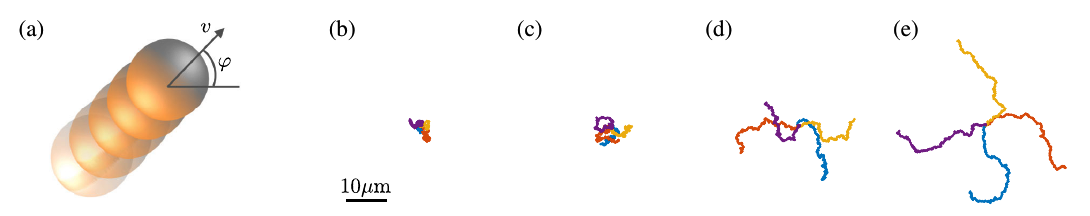
For Advanced Readers: Equations of Motion for an Individual Particle
The self-propelled motion of a single particle on a two-dimensional plane is given by an orientation angle $\varphi$ specifying the direction of motion and its constant absolute velocity $v$. In addition, both the position and orientation change by a Gaussian random process. The corresponding equations of motion are:
$$
\begin{align*}
\frac{\mathrm{d}x}{\mathrm{d}t}=v\cos\varphi + \sqrt{2D_T}\xi_x(t),\quad\frac{\mathrm{d}y}{\mathrm{d}t}=v\sin\varphi + \sqrt{2D_T}\xi_y(t),\quad\frac{\mathrm{d}\varphi}{\mathrm{d}t}=\sqrt{2D_R}\xi_\varphi(t).
\end{align*}$$
Here $(x,y)$, is the position of a particle in two dimensions, and $\varphi$ is the direction of the velocity. All $\xi_i(t)$ represent independent white noise stochastic processes with zero mean and $\delta(t-t^{\prime})$ correlations. The coefficients $D_T$ and $D_R$ are the diffusion coefficients of the translational and rotational Brownian motion, respectively.
The Vicsek Model
We now return to the Vicsek model and discuss what happens when more than one self-propelled particle moves on a plane with noisy aligning interactions. The motion and interactions of the particles are shown in Fig. 3: a particle ‘asks’ all other particles closer than a given radius (red circle) in which direction they are moving. That particle changes its orientation according to the average orientation of its neighbours, but makes a random error during the alignment. Therefore, the aligning process is not perfect, and the resulting orientation differs from the local average orientation in the particle’s neighbourhood. Then the particle moves in the direction of its new orientation, which leads to the neighbourhood being comprised of other particles. Thus, the particles change their interaction partners during the simulation.

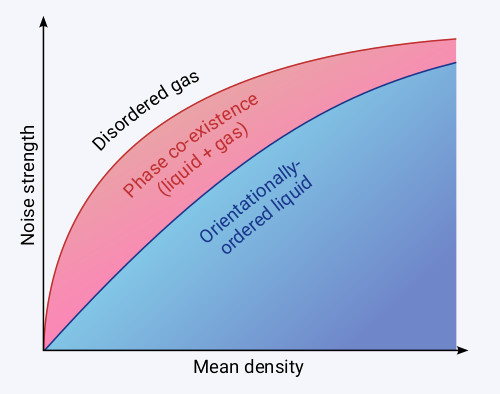
What happens in the simulations? The initial conditions are random, i.e., the particles are evenly spread throughout space, and their initial orientation can point in any direction, with all directions being equally likely. Therefore, the initial conditions are rotationally symmetric and the particles do not move coherently. The aligning interactions lead to orientational order, but the random error or noise destroys this order again. Thus, we distinguish an orientationally-ordered phase, in which all particles move coherently, and a disordered phase, in which the particles are equally likely to move in any direction. This is depicted in the phase diagram in Fig. 4. It shows the possible macroscopic phases of the flock depending on the mean density, i.e. the average number of particles in a given volume, and the noise strength, which is equivalent to the value of the so-called diffusion coefficient. For large noise strengths, the flock is in a disordered gaseous state and no coherent motion can build up. For low noise strengths, the flock turns into an orientally-ordered liquid phase. In other words, if the error each particle makes is low enough, the particles will move coherently in the same direction due to the aligning interaction. As the phase diagram suggests, the disordered phase and the orientationally-ordered phase depend on the noise strength compared to the mean density. That is because a higher density corresponds to more particles in the neighbourhood of each particle, making the alignment interaction stronger. Therefore, at higher mean densities, the noise strength must be higher to destroy the orientational order.
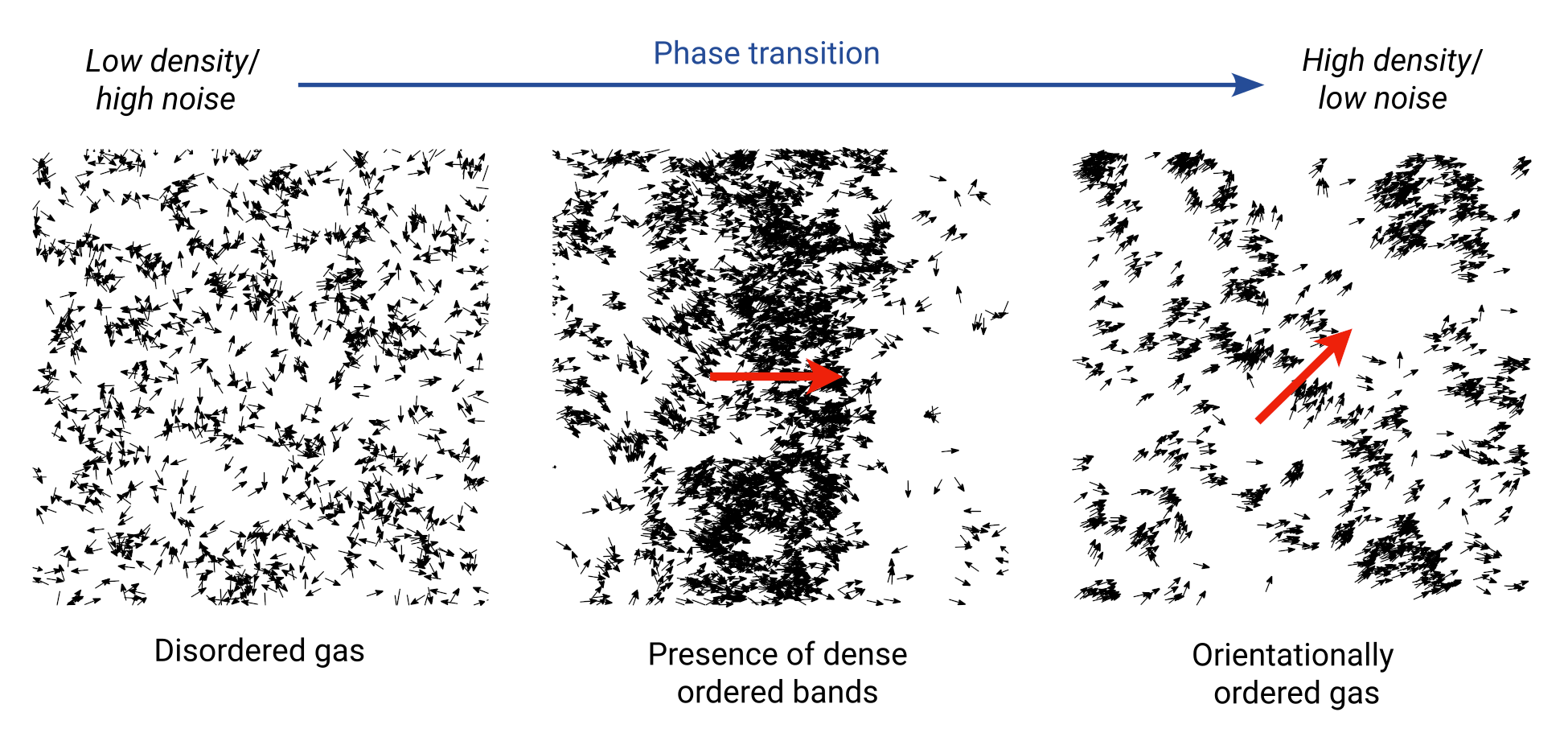
The disordered and orientationally-ordered phases are separated by a phase coexistence band. For intermediate combinations of the mean density and noise strength, one observes so-called phase-separation. This means that the system is partially ordered: one or several dense bands form that coherently move through a disordered gas. The disordered phase, the phase separation and the orientationally-ordered phase are shown in Fig. 5.
Why Is This Surprising?
So, in fact, the simple model by Vicsek et al. (1995) can account for the phenomenon of collective and coherent motion in systems of (many) self-propelled particles. The ingredients were particles moving at a constant absolute velocity, able to align their direction of motion locally by short-ranged interactions with their neighbours in the presence of noise. When the noise is weak enough, orientational order can emerge. In other words, the rotational symmetry can be broken and a single direction is preferred. Even in two dimensions! This is rather surprising from a statistical physics point of view, as we will see in the following.
Let’s have a closer look at the Vicsek model: the particles, by their direction of motion – which is also their orientation – are polar, i.e., they point in the direction of their velocity. The interactions are short-ranged and tend to align the orientations of neighbouring particles. This is very close to the XY model for a system of many magnets. The magnets are – by their magnetic field – polar and interact with their neighbours in a way that aligns their magnetic fields. This alignment is also subject to noise due to a non-zero temperature in such a magnetic system. For an equilibrium system in two dimensions with only short-ranged interactions, the continuous rotational symmetry cannot be broken. Put a little differently, for a two-dimensional system of magnets, which may point in any direction, with short-ranged interactions no orientational order will emerge at finite temperature in thermal equilibrium. This is the famous Mermin-Wagner theorem.
But why can orientational order emerge in the Vicsek model? The difference between the XY model and the Vicsek model is the fact that the self-propelled particles are moving. This makes flocks non-equilibrium systems. So even though the interactions are only short-ranged and alignment is subject to noise – all conditions of the Mermin-Wagner theorem – motion must be able to establish orientational order.
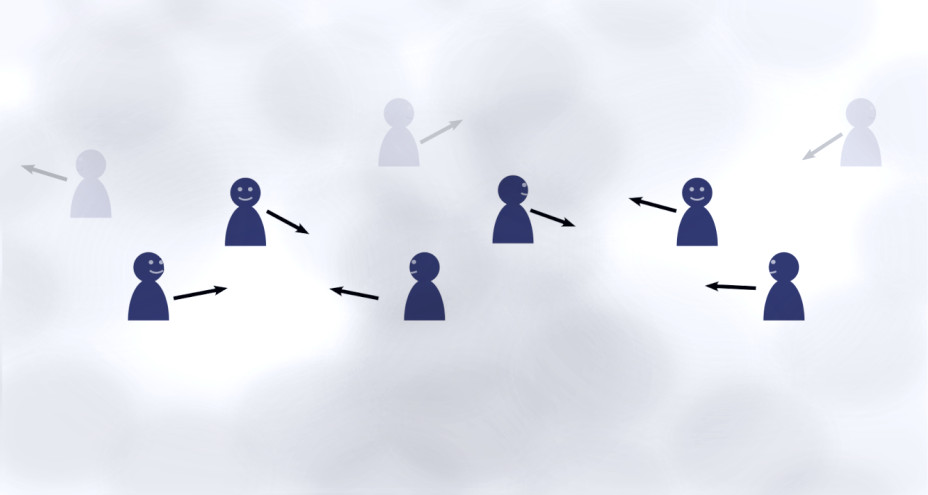
Following Toner (2019) we can conduct two gedankenexperiments that might make this clearer: imagine a featureless plane such that no direction is preferred to any other. This ensures rotational symmetry. Next place a large number of people homogeneously on that plane and let them be surrounded by fog. The fog reduces the sight of people, such that they can only see their nearest neighbours. In the two experiments, these people are given the task of (a) pointing in the same direction and (b) moving in the same direction (see Fig. 6).
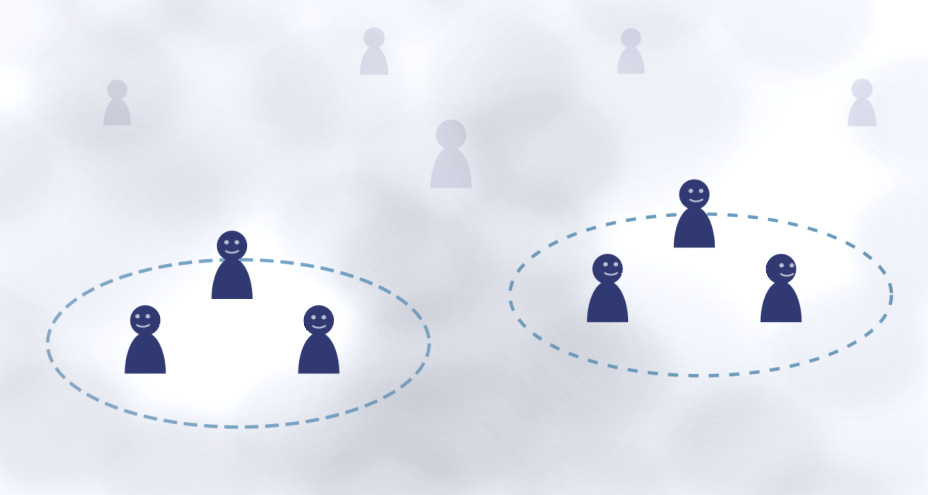
For experiment (a), everyone is stationary. Due to the fog, the pointing direction of people close to each other will align. Actually, if this alignment is not prone to errors, everyone will point in the same (but spontaneously chosen) direction. Let us assume the alignment is prone to errors, i.e., each person makes a random error while pointing in the same direction as their neighbours. The result is the following: while locally, i.e., in a person’s neighbourhood, people are pointing in almost the same direction, far away from this neighbourhood people are pointing in a completely different direction. That is because any error is propagated through all neighbourhoods. Very much like what happens when playing whisper down the lane.
For experiment (b), people are moving and aligning their direction of motion with their neighbours. This alignment may also be “noisy”. In contrast to experiment (a), orientational order will be established because now neighbourhoods are mixing. As people move through the fog, their neighbourhoods change: people previously too far away to be seen by a person become visible as they are moving closer together, while other people vanish from the neighbourhood. Due to this fact, the alignment or preferred direction is moving faster through the fog than any error is, and orientationally-ordered motion can emerge.
Outlook
The Vicsek model is a simple and minimal model for flocking behaviour. It emulates systems of living organisms, such as birds or bacteria, by self-propelled/active particles. These particles convert energy locally into directed motion with a constant absolute velocity. Noisy interactions with their neighbours tend to align the orientation of the particles’ motion. For weak enough noise, orientational order is achieved and collective, coherent motion occurs.
This model acts as a baseline for modelling and understanding collective phenomena in systems of living organisms. Therefore, changes in the model are necessary to mimic real living systems. For animals, such as birds or fish, one has to limit the interactions to only those neighbours that can be seen by an individual. Depending on the animal’s eye-sight, it can only see a limited fraction of the space around it, which is usually referred to as the visual cone. For bacteria, the hydrodynamic interactions with the surrounding medium become relevant. For a relationship between observations and models, see Vicsek & Zafeiris (2012).
The Vicsek model is a minimalistic model for understanding collective properties of active particle systems, and the model’s features may be changed. For example, the interactions do not have to be specifically aligning the particles’ orientations. Instead, collisions between particles may occur in the presence of some interaction potential. This potential may be attracting (keeping particles close together) or of volume exclusion (keeping particles from approaching too close), cf., Vicsek & Zafeiris (2012).
The Vicsek model does not conserve momentum by design, since the particles never change their absolute velocity. This is often referred to as a dry active system, since there is no momentum exchange with the fluid surrounding the particles. This is a valid assumption for organisms moving on a substrate. A valid modification to the Vicsek model is taking into account the effects of the bulk fluid in which the self-propelled particles are moving. Interactions between the particles and the surrounding medium again introduce momentum conservation.
References
- T. Vicsek, A. Czirók, E. Ben-Jacob, I. Cohen, O. Shochet, Phys. Rev. Lett. 75:1226 (1995)
- J. Toner, Y. Tu, Phys. Rev. Lett. 75:4326–29 (1995)
- T. Vicsek, A. Zafeiris, Physics Reports, Volume 517, Issues 3–4 (2012)
- C. Bechinger et al., Rev. Mod. Phys. 88, 045006 (2016)
- F. Ginelli, Eur. Phys. J. Special Topics 225, 2099–2117 (2016)
- J. Toner, Why walking is easier than pointing: Hydrodynamics of dry active matter, arXiv:1812.00310 (2018)
- H. Chaté, B. Mahault, Dry, aligning, dilute, active matter: A synthetic and self-contained overview, arXiv:1906.05542 (2019)
Tags:
Collective Phenomena
Self-Organization
Correlations
Biophysics
Symmetry
Statistics
Phase Transitions
Thermodynamics