STRUCTURES Blog > Posts > Let's pack up our spheres and go!
Let's pack up our spheres and go!
To the layman mathematics often is an obscure and inscrutable exercise of sheer abstraction. The truth is, however, that a lot of deep and advanced mathematics is born out of very simple and down-to-earth problems. The sphere packing problem is one of these.
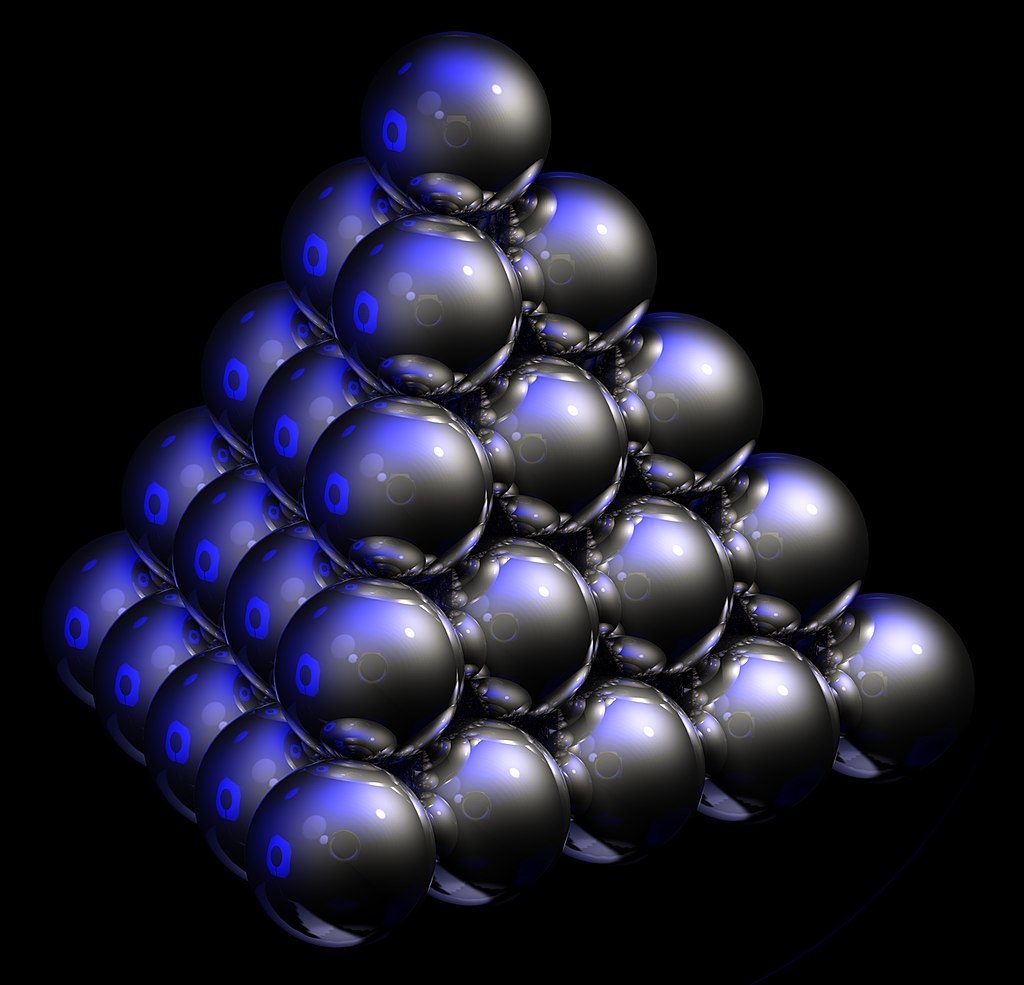
Suppose that a vendor has a certain quantity of oranges to be arranged in a box. What is the arrangement that maximizes the number of oranges that fit the box?
In order to solve the problem, one has to first make some simplifications, such as assuming the oranges are spheres of the same size, which is small compared to the size of the box. One way of approaching the problem is the following: arrange the spheres on a first horizontal layer A, then add a second layer B where each sphere sits atop the hollows left in the first layer, then repeat this configuration AB AB AB AB…. This is the so-called Hexagonal Close-Packing (HCP).
The Hexagonal Close Packing (HCP) fills up about 74% of the space
However, this is not the only possible arrangement. One can obtain another arrangement as follows: start with a first horizontal layer A, add a second layer B where the sphere sits in the voids of A as before, add a third layer C where the sphere are shifted by one with respect to the sphere of A, then eventually repeat the configuration: ABC ABC ABC …. This arrangement is called Face-Centered Cubic Packing (FCC) or cubic close-packing.
One can compute the density of FCC and find that it’s the same density of HCP.
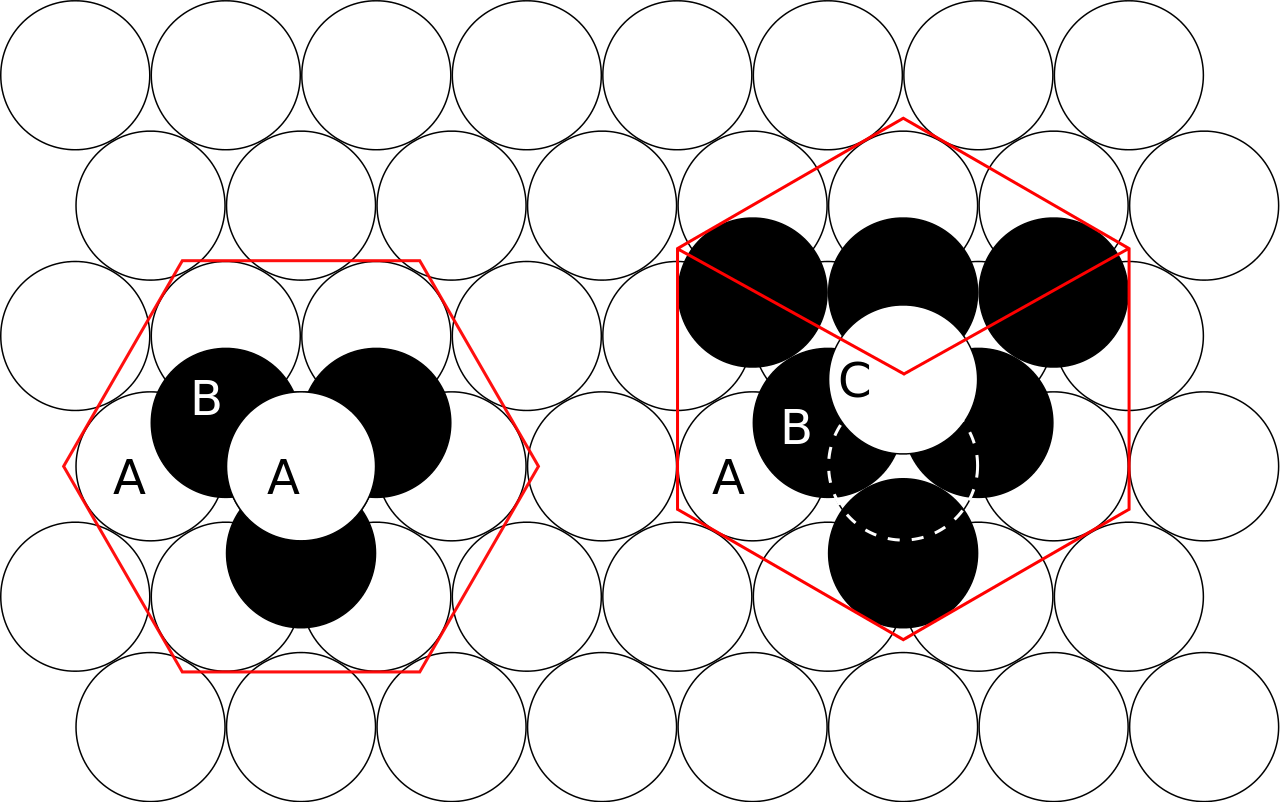
However, since there are exactly two distinct ways to place a layer of spheres on the top of a given one, there are infinitely many possible packings (Barlow packings), which realize different densities.
Packing of spheres have always been considered interesting for many reasons. For instance, many crystal structures are based on sphere packings of atoms or ions. Other examples of sphere packing problems come from the military. The classical cannonball problem, which asks which flat square arrangements of cannonballs can be stacked into a square pyramid, dates back to the late 16th century. Only in 1875 Eduard Lucas reformulated the problem as: find all pairs of integers $(N,M)$ such that
$$\frac{1}{6} N(N+1)(2N +1) = M^2,$$
where $N$ is the number of layers in the arrangement and $M$ is the number of cannonballs along an edge in the flat square arrangement. He conjectured that the only solutions are $(1,1)$ (with 1 cannonball) and $(24, 70)$ (with 4900 cannonballs). His conjecture was proved only in 1913 with sophisticated methods in number theory.

A famous conjecture by Kepler states that no arrangement of equally sized spheres filling space has a greater average density than that of the cubic close packing (face-centered cubic) and hexagonal close packing arrangements. This conjecture dates back to 1611, but it was proved only in 1998 with a heavily computer-assisted proof by Thomas Hales, who built on previous results by Fejes Tóth (1953). A natural mathematical generalization of the Kepler conjecture asks what is the optimal arrangement for spheres of equal size in a Euclidean space of dimension $N$. This is the so-called sphere packing problem.
The idea of working with 10 or 100-dimensional spaces might sound exotic or scary to many. While none of us is going to eat a 10-dimensional orange soon, it’s important to understand that for scientists the dimension of a space is simply the number of parameters that they need to describe it: in a 2D-space, every point is described by 2 coordinates; in a 3D-space every point is described by 3 coordinates; in a 4D-space one needs 4 coordinates; in a general $N$-dimensional space any point can be described by $N$ coordinates, where $N$ is some given number.
In mathematics a sphere in a space is just a set of points that have constant distance from a given point. Spheres in any dimension can be described by very basic equations. In school, one might have encountered the equation of a sphere of radius $R$ centered in the origin of the 3D space:
$$ S^2 = \{ (x_1, x_2, x_3 ) \in \mathbb R^3 ~|~ x_1^2 + x_2^2 + x_3^2 = R^2 \}. $$
Similarly, a sphere in a 2D dimensional space has equation:
$$ S^1 = \{ (x_1, x_2) \in \mathbb R^3 ~|~ x_1^2 + x_2^2 = R^2 \}. $$
A sphere of radius R in the origin of a 4D space is described by :
$$ S^3 = \{ (x_1, x_2, x_3, x_4 ) \in \mathbb R^4 ~|~ x_1^2 + x_2^2 + x_3^2 + x_4^2 = R^2 \}. $$
In dimension 5, instead we found :
$$ S^4 = \{ (x_1, x_2, x_3, x_4, x_5 ) \in \mathbb R^5 ~|~ x_1^2 + x_2^2 + x_3^2 + x_4^2 + x_5^2 = R^2 \}. $$
and so on…
While the sphere packing problem is easy to formulate, it is incredibly difficult to solve. In 2D the optimal packing has long been known to be the one associated with the honeycomb lattice, achieving a density of more than 90%, from the works of Thue in 1910 and Fejes Tóth in 1943. Kepler’s conjecture in 3D was proved only in 1998 with a heavily computer-assisted proof by Thomas Hales, who built on previous results by Fejes Tóth (1953). In general, very little is known about the sphere packing problem for dimensions larger than 3.
This year Maryna Viazovska was awarded the most prestigious mathematical prize, the Fields Medal, for her solution of the sphere packing problem in dimensions 8 and 24. She is the second woman in history to receive the prize. Here you can watch a short video about her and learn more about her work.

Packings in high dimension are important for practical applications, in particular error-correcting codes for radio signals. Mathematical methods of encoding messages to ensure correctness when transmitted over noisy channels rely heavily on sphere packings in high-dimensional spaces. The dimension of the space is the number of measurements used to characterize the signals. For more about this kind of application, you can read this beautiful article.
Acknowledgements: the article relies in part on a previous article I co-authored and published on the EGMO 2018 blog http://www.egmo2018.org/blog/wimbs-maryna-viazovska/
Tags:
Mathematics
Geometry
Women in Science