Do you think you can tell… a doughnut from a cup?

Topology is the branch of mathematics which studies the “shapes” of the objects. The geometry that people study in school typically deals with “exact” measurements of angles, lengths, areas, or volumes. We know that from the point of view of Euclidean geometry, a right-angled triangle is “different” from an equilateral triangle, a square is “different” from a circle.

Unlike geometry, topology thinks of objects as made of “rubber”: an object can be stretched, bent, contracted but not broken or cut. For example, a square can be deformed into a circle without breaking it, but a figure 8 cannot.

But how do we know this? Mathematics is full of obscure and counter intuitive examples which defy reality. In this case, mathematicians found an »invariant« for shapes which tells us if two surfaces can be deformed into another by application of the above rules. An invariant is a quantity associated with an object, which does not change under the imposed rules. In our case: bending and stretching does not change this quantity. In the following, we want to show how you can think of this invariant.

In school you might have heard of Platonic solids, that is, polyhedra whose faces are regular polygons of the same type and size with all vertices lying on the same sphere. There are very few of them and they are: the cube, the dodecahedron, the icosahedron, the octahedron, and the tetrahedron.

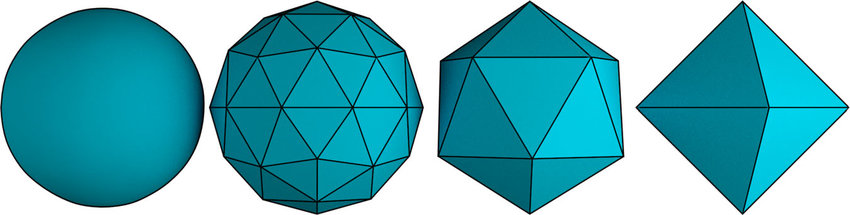
Any Platonic solid can be deformed into a sphere by “pushing” its faces.

A funny joke says that topologists are people who cannot distinguish a coffee cup from a doughnut:

(Segerman: https://www.youtube.com/watch?v=9NlqYr6-TpA )

A powerful invariant to distinguish the topology of objects is a number called Euler Characteristic.
The Euler characteristic $\chi$ of a polyhedron P is defined according to the formula
$$
\chi = V - E + F, $$ where $V$, $E$, and $F$ are respectively the numbers of vertices, edges and faces of P. The Euler characteristic was first defined and studied by the mathematician Leonhard Euler in 1778. In the case of the Platonic solids the computation is in the table below.

Name	Image	Vertices $V$	Edges $ E $	Faces $ F$	Euler characteristic $ V − E + F$
Tetrahedron		4	6	4	2
Cube		8	12	6	2
Octahedron		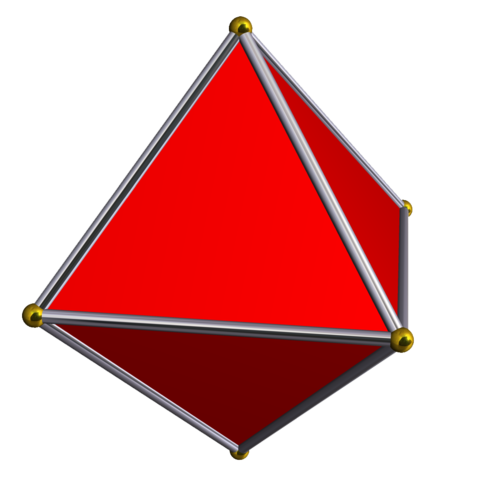6	12	8	2
Dodecahedron		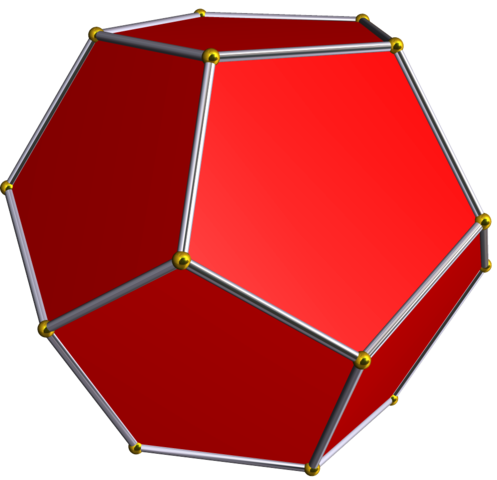20	30	12	2
Icosahedron		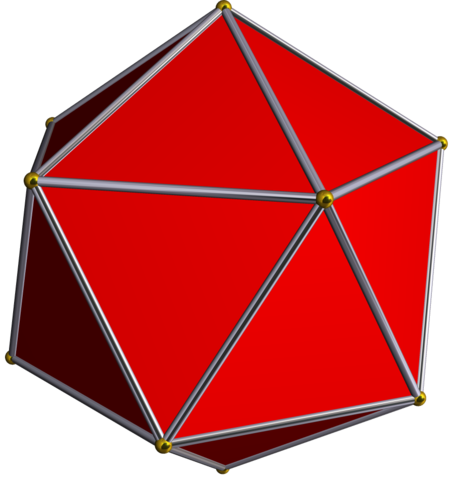12	30	20	2

Euler actually proved that all convex polyhedra have Euler characteristics 2. This result can actually be generalized for larger 2-dimensional objects, the surfaces.

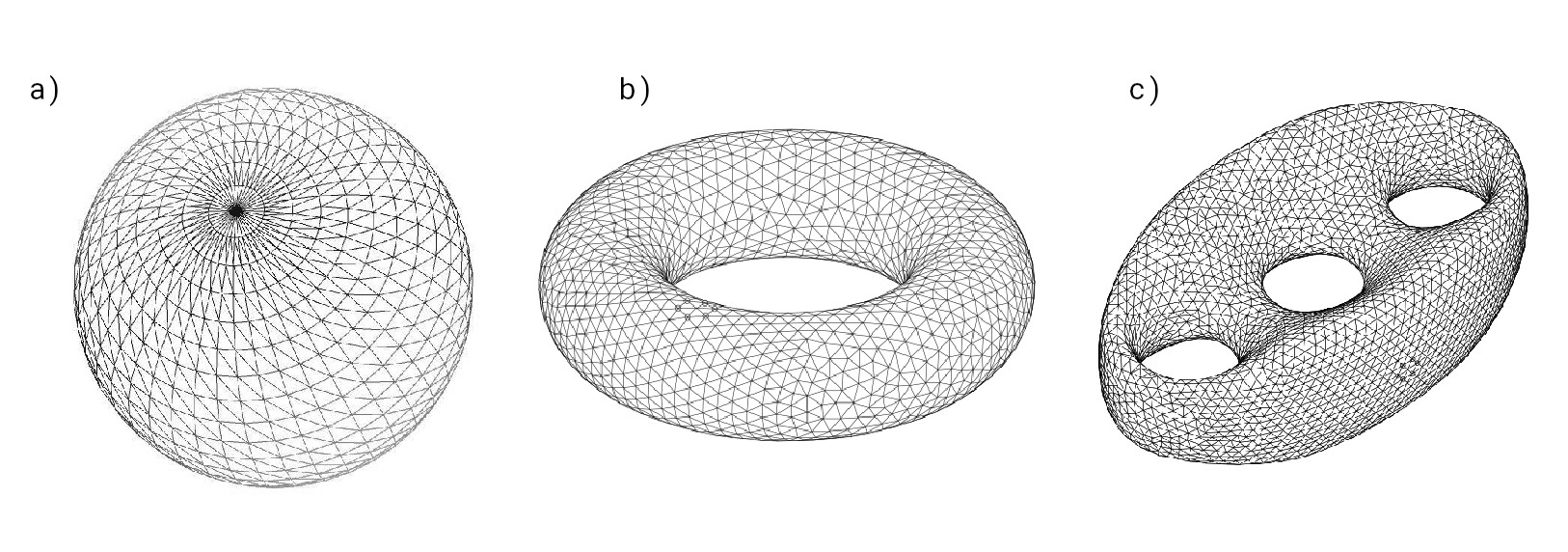
A surface is an object obtained gluing together pieces of the plane. In the figure above, each one of the three surfaces is obtained gluing together triangles along a common edge. Polyhedral surfaces are particular examples of surfaces which are topologically equivalent to a sphere.

Actually, the Euler characteristic can classify all the shapes of surfaces. Indeed, an important theorem in mathematics says that every surface is homeomorphic to a sphere with some “handles” and the Euler characteristic of a surface is always equal to $\chi = 2 - 2g$, where $g$ is the number of “handles” of the surface.

(The two surfaces below are topologically equivalent.)

    

In other words, two surfaces are topologically equivalent if and only if they have the same Euler characteristic. In the table below we list some computations:

Name	Surface	Euler Characteristic
Polygon		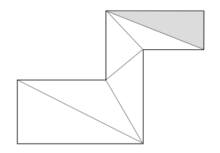1
Sphere		2
Torus		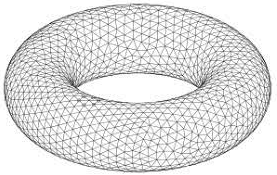0
Double torus		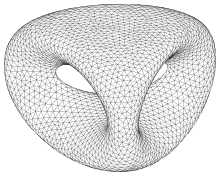−2
Triple torus		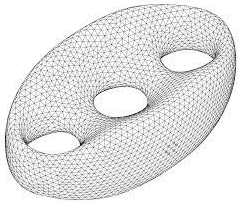−4

As a final answer, we can now say that the three surfaces we showed above are not topologically equivalent.