What Psychiatric Disorders Have to do With Dynamical Systems

Perhaps you can relate to situations in which you may have caught yourself pondering excessively about something unpleasant, and, although deliberately shifting attention to something else, your mind repeatedly kept wandering back to those thoughts. Or, you may have felt so emotional (or angry) that - in that very moment – you were unable to accept any other but your own perspective, unfit to detach from your own thoughts and judgments, or control your anger. Although these examples are common phenomena that many of us experience in everyday life, when they intensify and persist, they can threaten mental well-being. In fact, mental disorders such as Major Depressive Disorder, Generalized Anxiety Disorder, or Borderline Personality Disorder often experience similar symptoms of rumination and emotion dysregulation [1, 2].

You might be surprised to learn that these mental phenomena share some intriguing similarities with the behaviour of dynamical systems – a concept known from mathematics. A dynamical system describes how the state of a system changes over time based on a set of rules or equations. Depending on the specific equations that govern the system, dynamical systems can exhibit various types of behaviour. For instance, they can harbour different forms of attractors, regions in a system’s state space (i.e., the space spanned by the system’s dynamic variables) that attract and, with time, fully absorb neighbouring states within their basin of attraction (the attracting vicinity of the attractor). Unless intrinsic noise or external events push the system out of an attractor’s basin, it will remain there indefinitely. Depressive or anxious thoughts that an individual repeatedly returns to and ruminates on, resemble that of attracting dynamics [3, 4]. Often individuals report to be drawn in and consumed by such thoughts. Along similar lines, intruding memories (so-called intrusions) can haunt soldiers that have endured traumatic events during combat and suffer from Post-traumatic Stress Disorder.

The resemblance between symptoms of mental disorders and dynamical system phenomena is not a coincidence. After all, we still believe psychiatric symptoms emanate in the brain, and the brain is in fact a densely connected network of billions of neurons that collectively form a nonlinear dynamical system. Computational neuroscientists have advocated for decades that cognitive functions are implemented in the dynamics of this network, with attractor landscapes underlying multiple cognitive phenomena including, among others, working and associative memory [5, 6], decision making [7], action sequences [8], and bistable perception [9]. Following this stance, mental illness and cognitive dysfunction may emerge through alterations in attractor geometry (or more generally network dynamics) [10].

Attractors underlying rumination, intrusive, or obsessive compulsive thoughts, for instance, are likely altered in a way that they draw in many more ‘mental’ states (i.e., are wider), perhaps exerting a stronger pull (i.e., are steeper), when compared to those of healthy individuals. See for instance the illustration in Fig. 2. A person ruminates when positioned in the left attractor. In locations close to the attractor, within its attractor basin, the person is drawn back into the ruminating state. We can envision this by fictitiously positioning a ball close to the attractor state – it will automatically roll down the well to its lowest point. In the pathological case (right image), the basin of attraction is wider and therefore many more mental states will result in rumination. It is also steeper; we require a lot more energy to push the person out of the ruminating state. Such alterations could mechanistically explain why some patients may have such a hard time letting go of thoughts, actions, and emotions.

Whether all psychiatric symptoms will one day be explained in terms of aberrant network dynamics is of course an open question. And it is not a simple one. To assess attractor dynamics in the diseased brain, we require a valid mathematical model of the brain (or parts thereof), that is, equations that precisely mimic its dynamics, and that we can then dissect and analyze in detail. Many existing approaches use models that behave ‘similar to the brain’ in some statistical sense, but not necessarily similar in terms of reconstructing (parts of) a system’s trajectories or its vector field (determining the change of the state variables at each point in state space). The Theoretical Neuroscience Department and my research group Computational Psychiatry focus on advancing models that are specifically geared towards the latter, that is, to infer models of the brain that aim to mimic the precise underlying data-generating mechanisms, (attracting) dynamics, and long-term behaviour [11-13]. We call this dynamical system reconstruction [14].

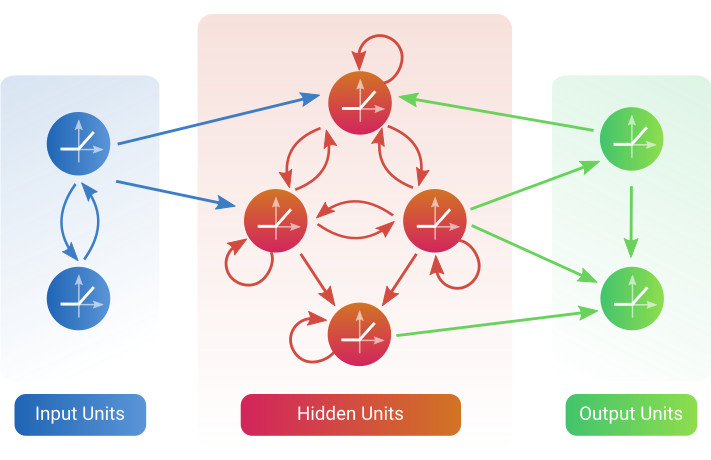
Most of these models make use of recurrent neural networks (RNNs). RNNs are efficient tools to approximate nonlinear dynamical systems, and can autonomously learn to represent dynamics based on observed time series like time series recorded from the human brain, reflecting neuronal activity. This has to do with the fact that, unlike feedforward network models that solely exhibit forward connections, RNNs share recurrent connections. Recurrence allows RNNs to store memory (as needed to represent temporal dependencies) and makes them structurally somewhat similar to the wiring of the brain. It also makes them dynamical systems themselves. A simplified sketch of a general RNN architecture is shown in Fig. 3, illustrating different possibilities of how units may connect to each other.

Applying this approach in the context of psychiatry, we hope to advance our understanding on the pathophysiology underlying psychiatric disorders in multiple ways. As outlined earlier, we can use the approach to identify and understand altered dynamics and associated pathological neural mechanisms underlying psychiatric symptoms, as well as to distinguish diseased and healthy brains based thereon [15]. Moreover, we could predict tipping points in the neural data that can explain sudden onsets or offsets of symptoms such as the sudden onset of an epileptic seizure, for instance. Finally, we may aim to identify treatments capable of restoring aberrant dynamics, e.g., by simulating how neural dynamics change in response to real or hypothetical perturbations, or by evaluating the effect of psychopharmacological drug treatments.

Naturally, there is much more to say on how cognitive function and mental health symptoms relate to network dynamics, how it all relates to what we know about altered neurobiology in psychiatry, and what is required for dynamical system reconstruction. RNNs, moreover, can come in handy in multiple health-related domains other than ‘just’ mimicking brain function, including the data-driven analysis of behaviour [16]. We hope though that with this blog post we were able to motivate how the reconstruction of brain dynamics may be helpful, maybe even indispensable, to understand pathologies of the human mind.

For Advanced Readers: Analyzing Human Imaging Data

Say we have collected a multivariate (and possibly multimodal) time series $ X = \{ x_1, x_2, \dots , x_T \} $, with $ x_t \in \mathbb R^N $. This could correspond to a neural time series of brain regions of a human participant recorded with the functional magnetic resonance imaging (fMRI) device during the presentation of a cognitive task. We would then like to train an RNN model on these measurements $ X$.

Taking an RNN of the (rather) general form

$$ z_t = A z_{t-1} + W {\varphi} ( z_{t-1}) + h + C s_t + \epsilon_t, \quad \epsilon_t \sim N( 0, \Sigma) $$

where $ z_t \in \mathbb R^M$ represents the (latent) system state, $ A, W \in \mathbb R^{M \times M}$ are diagonal/off-diagonal transition matrices, ${\varphi}$ is a nonlinear activation function (such as a rectified linear unit (ReLU), see also Fig. 3), $ h$ is a bias term, $ s_t \in \mathbb R^K$ are external inputs which affect the latent state via regression coefficients $ C \in \mathbb R^{M \times K}$, and $ \epsilon_t$ is Gaussian noise with covariance matrix $ \Sigma$, and tying it probabilistically to our measurements, e.g., via a Gaussian process

$$ x_t \vert z_t \sim N( g_{\lambda}( z_t), \Gamma ), $$

we obtain a state space model that we can infer via Variational Inference or the Expectation-Maximization framework.

After inference, we can verify our dynamical system reconstruction by checking whether the true and reconstructed systems agree in time-invariant properties, that is, properties that do not depend on when we actually measure [14]. For instance, we may want to look at the overlap between the true and generated data/state distributions in the temporal limit (i.e., when the systems are expected to converge towards time invariant sets like attractors).

If the reconstruction was successful, we can use the inferred RNN as a formal surrogate to study brain dynamics. For instance, we can have a look at different attractor objects and their basins of attractions. For RNNs with ReLU activation functions, we can sometimes analytically solve for the presence of different attractors of the autonomous system [11, 17]. We may also want to examine the connectivity parameters $( A, W)$ in detail, or simulate effects of true or hypothetical external perturbations on system dynamics by applying a stimulus $ s_t $ and running the RNN forward in time. Finally, and not exhaustively, we may want to extract RNN features and run classification or regression analyses for different patient populations.

Literature