From Ants to AdS

There is a well-known riddle that can be stated as follows: suppose you have a stick of length $L$ with a number of $N$ ants placed on it. The ants can move with constant speed $v$ either to the left or the right. If two ants collide, they each change their direction instantaneously and if an ant reaches the end of the stick, it falls down and is never to be seen again. The question to be addressed: given an initial condition of ants, how long does it take until the stick is empty?

At first sight, this appears to be a fairly complicated problem. The ants are changing directions all the time and tracking their motion is a big mess. However, — as is often the case with these kinds of riddles — there is a neat trick. Imagine the process of two ants colliding. They’re coming closer and closer, touch for an instance, change directions and then each go their way. To solve our problem, there’s no need to distinguish individual ants: we only want to know when the last ant is gone (also, who can tell one ant from another?). Now imagine the ants come closer and closer and then just pass each other. Can you tell the difference from them colliding? Of course not: as the ants are indistinguishable, the two processes are exactly the same. But this renders our problem almost trivial. For the ants just passing each other, it’s easy to figure out when the stick is going to be empty. Just take the ant initially facing the longest distance $d$ and use $t = d/v$.

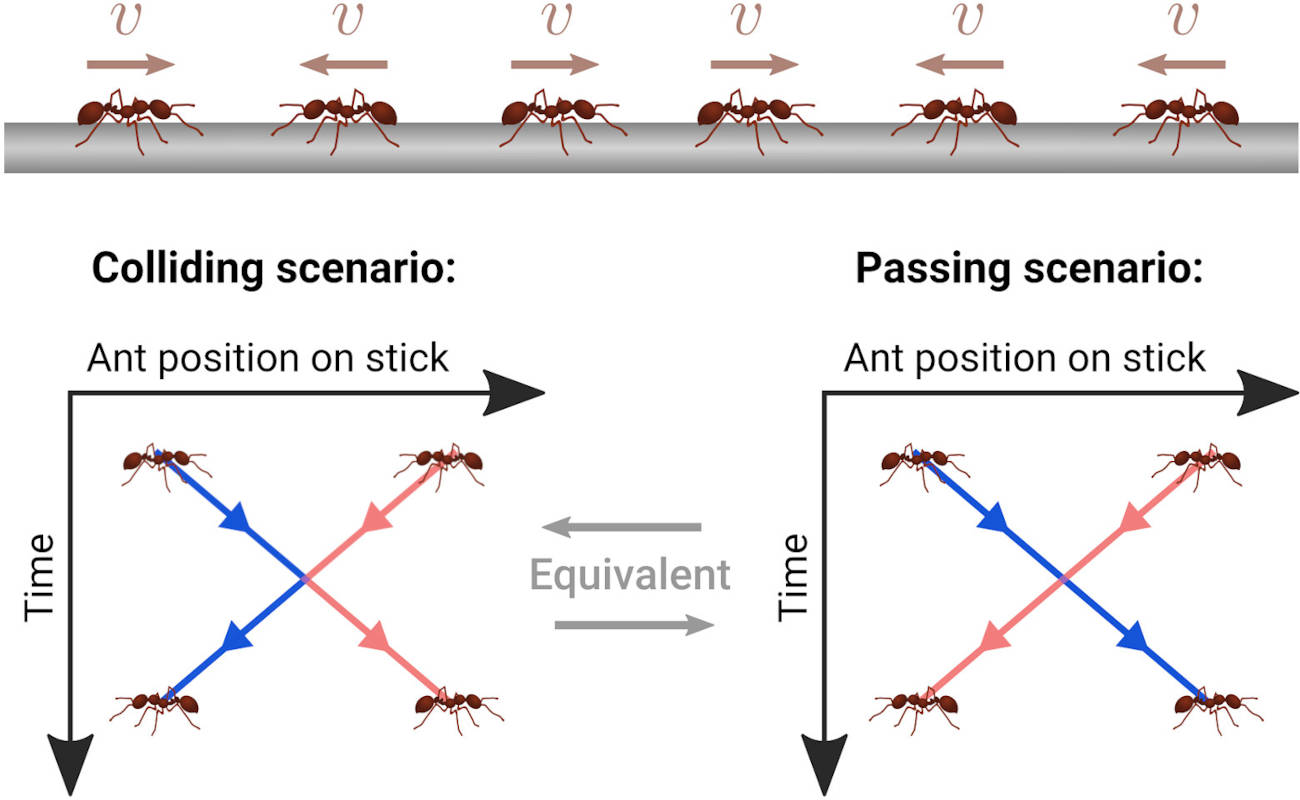
What we witnessed in this problem is a duality principle. We gave two different physical models (one with the ants colliding and one with them passing), which—at first sight—seem at odds with each other, but actually turn out to be equivalent descriptions of one underlying reality (indistinguishable ants moving on a stick). This is, of course, remarkable, as it transforms a difficult problem that is hard to grasp (ants colliding) into a simple one (ants passing). Such behaviour is characteristic for “strong-weak” dualities. In general, the strength of interaction in a physical model is described by a parameter $g \in \mathbb R$ called the coupling constant. Under a strong-weak duality two models with coupling constants $g$ and $g’$ are equivalent via an identification of the form $g’ = 1/g$, which means that if $g$ is very small, then $g’$ is very large and vice versa. Thus, strongly coupled dynamics in the first model is equivalent to weakly coupled one in the second. Note that this is exactly what happens in our example. A strongly coupled system ($g = \infty$; the ants interact via perfectly elastic scattering) is mapped to a system with no interaction at all ($g’ = 1/g = 0$; the ants don’t interact).

Naturally, the relevance of dualities in physics reaches far beyond ants moving on a stick. One of the most interesting examples in contemporary physics is the AdS/CFT-correspondence. This duality equates certain gravity theories in negatively curved spacetime (Anti-de Sitter space, or AdS) with particular field theories (i.e. conformal field theory, CFT) without gravity in a lower dimensional world.

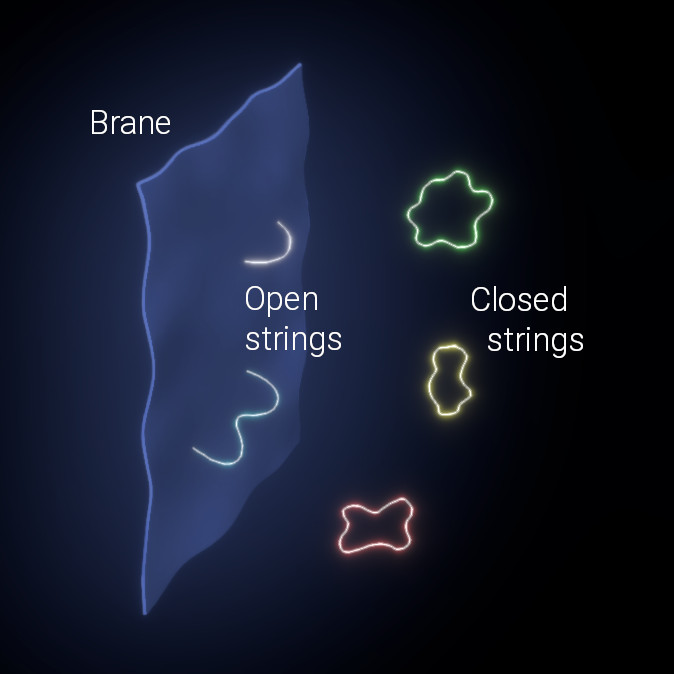
At first sight, these two theories seem unrelated, but that’s what makes a duality interesting: two descriptions, seemingly in conflict, incompatible, or entirely unrelated, turn out to be equivalent by viewing them as different aspects of an underlying physical system. In the case of AdS/CFT, this underlying physical system is one of strings and D-branes. From the point of view of the gravitational side of the duality, branes are objects with tension and energy; their interplay with strings is described by a gravity theory. Meanwhile, the conformal field theory perspective uses branes as boundary conditions for open strings. This leads to a description in terms of a field theory on the brane. Viewing both as instances of the full string/brane system, both descriptions are equivalent. Again, as in the example of the ants, this is a strong-weak duality and it has the important advantage of translating questions in strongly coupled field theories (which are very difficult), into easier ones in terms of weakly coupled gravity where semi-classical approximations are appropriate.

Even besides turning difficult problems into easier ones, dualities are extremely useful in transferring insights from physics into pure mathematics. To each physical system, there is a bunch of mathematical structures attached, most notably the collection of observables (i.e. the measurable quantities), but also the configurations and boundary conditions. If there is a duality between two physical models, this implies that there also is a correspondence between the associated mathematical structures. As physical models on either side of the duality can look very different, this often leads to fascinating relations between areas of mathematics seemingly unrelated at first sight.

There is one caveat though: in the context of quantum field theory, let alone string theory, a rigorous understanding of the full mathematical structures on the different sides of the interesting dualities is usually unavailable. However, there is a way out: twisting!
To explain how this works we have to digress a little. Dualities often occur in highly symmetric settings. We already saw this in our introductory example: the ants had to be indistinguishable. If we would break that symmetry, for example by colouring them in red and blue and then asking when the last red ant is falling off the stick, our duality ceases to work. Above, we described the AdS/CFT duality, which is situated in a highly symmetric setting. Such situations have protected subsectors (smaller parts of the theory) that are usually much easier to understand and describe mathematically. Twisting is a procedure to restrict the (physical) theory to such (mathematically tractable) subsectors in a compatible manner. Crucially, twisting on both sides of a duality establishes a correspondence between these subsectors – and hence a correspondence between their associated mathematical structures.

A success story in that regard is mirror symmetry. This is a duality arising between strings in different backgrounds, so-called mirror dual Calabi–Yau pairs (see also Fig. 4). In the twisted setting, the two theories that are equivalent via duality (dubbed the A model and the B model) are sensitive to very different geometric structure of their respective backgrounds. The geometric structure in the A model is called symplectic, while the one in the B model is called complex. This is a fascinating relation between two different types of geometries unified under the umbrella of string dynamics.

Understanding the mathematical implications of the AdS/CFT duality is an ongoing effort in physical mathematics, summarized under the term “twisted holography”. Much progress in that direction has been made in the last years, but there are still many connections to be explored, mathematical correspondences to be worked out, and riddles to be solved.

References

[1] J. Maldacena. The Large N Limit of Superconformal Field Theories and Supergravity. Adv. Theor. Math. Phys., 1998. arXiv:hep-th/9711200.