STRUCTURES Blog > Posts > The Palace of Alhambra and the Crystallographic Groups
The Palace of Alhambra and the Crystallographic Groups

I first learned about tilings during my last year of the bachelor’s program. At the time Dr. Pellicer was in charge of the class on Selected Topics in Combinatorics, and from then on, tilings held a very special place in my mathematical heart.
A tiling (or tessellation) is a covering of the plane by copies of pieces of the plane that don’t overlap. More precisely, one starts with a collection of subsets $ \{ T_1, T_2, \dots \} $ (not necessarily finite, although for this post, it doesn’t hurt to assume the set is finite) of the plane called tiles, and a tiling consists of an arrangement of copies of $T_i$ in $\mathbb R^2$ so that:
- The union of all these copies is the plane, and
- The interior of the tiles is pairwise disjoint.
The following pictures show an example and a non-example of a tiling.


(On the right) The picture shows the front of the Mathematical Sciences Research Institute in Berkeley, USA. If the tiles are two Penrose rhombi (the thin rhomb has two angles of 36° and two of 144°, while the thick rhomb has two angles of 72° and two of 108°), then the arrangement is not a tiling, due to the spaces in white.
But how can we study such mosaics from a mathematical point of view? One way is to associate each tiling with its group of symmetries. Given a tiling by tiles $ \{ T_1, T_2, \dots \} $, a symmetry $ \phi $ is a rigid motion of the plane (that is, a function from $\mathbb R^2$ to itself that doesn’t change distances in the plane) so that each $\phi(T_i)$ coincides again with some $T_j$. The set of all the symmetries of a given tiling forms a group, with the composition of functions as the group’s operation.

Some tilings may look different, but they have the same group of symmetries. But that is fine: after all, by studying their symmetry group, we are really looking at the structure that governs the distribution of the tiles.

Wallpaper Tilings
Among all tilings, there is a particular type called wallpaper tilings. A wallpaper tiling possesses two translations in linearly independent directions as symmetries. But they can also have other symmetries!
Among rigid motions, apart from translations, we have:
- Rotations by an angle $\theta$ between $0$ and $2 \pi$ centred at a point $p = (p_1, p_2)$,
- Reflections over a line, and
- Glide reflections, which are reflections over a line, followed by a translation along the direction of the axis of reflection.
The groups of symmetries of wallpaper tilings are called plane crystallographic groups.
And it turns out plane crystallographic groups don’t admit as many symmetries as one could initially think. In 1891, Evgraf Fedorov proved there are precisely 17 plane crystallographic groups: the group of symmetries of any given wallpaper tiling is one of the following in the table:
| Notations for a crystallographic group | Rotations of period | |||||||
|---|---|---|---|---|---|---|---|---|
| Hermann-Mauguin symbol | Orbifold notation | Glide-reflections | Reflections | 2 | 3 | 4 | 6 | |
| p1 | o | 0 | 0 | 0 | 0 | 0 | 0 | |
| pg | xx | 2 | 0 | 0 | 0 | 0 | 0 | |
| pm | ** | 0 | 2 | 0 | 0 | 0 | 0 | |
| cm | x* | 1 | 1 | 0 | 0 | 0 | 0 | |
| p2 | 2222 | 0 | 0 | 4 | 0 | 0 | 0 | |
| pgg | 22x | 2 | 0 | 2 | 0 | 0 | 0 | |
| pmg | 22* | 1 | 1 | 2 | 0 | 0 | 0 | |
| pmm | *2222 | 0 | 4 | 4 | 0 | 0 | 0 | |
| cmm | 2*22 | 2 | 2 | 2 | 0 | 0 | 0 | |
| p3 | 333 | 0 | 0 | 0 | 3 | 0 | 0 | |
| p31m | 3*3 | 1 | 1 | 0 | 2 | 0 | 0 | |
| p3m1 | *333 | 1 | 1 | 0 | 1 | 0 | 0 | |
| p4 | 442 | 0 | 0 | 1 | 0 | 2 | 0 | |
| p4g | 4*2 | 2 | 1 | 1 | 0 | 1 | 0 | |
| p4m | *442 | 1 | 3 | 1 | 0 | 2 | 0 | |
| p6 | 632 | 0 | 0 | 1 | 1 | 0 | 1 | |
| p6m | *632 | 2 | 2 | 1 | 1 | 0 | 1 | |
Given a wallpaper tiling, it is common to illustrate its symmetries by using the symbols in the following table.
| Symbol | Meaning |
|---|---|
 | Line of reflection |
 | Line of a glide reflection. |
 | Centre of a 2-fold rotation. |
 | Centre of a 3-fold rotation. |
 | Centre of a 4-fold rotation. |
 | Centre of a 6-fold rotation. |
 | Centre of a 2-fold rotation lying on a line of reflection. |
 | Centre of a 3-fold rotation lying on a line of reflection. |
 | Centre of a 4-fold rotation lying on a line of reflection. |
 | Centre of a 6-fold rotation lying on a line of reflection. |
Groups of Symmetry
P1: Only Translation Symmetries
Tilings with a group of symmetry p1 are the ones that show the least amount of symmetries. Their symmetry group is generated by two translations in linearly independent directions. The picture shows two vectors representing the directions of two symmetry translations.

All other wallpaper tilings possess more than just two translations as symmetries, so we will indicate the other symmetries they have.
Pg and Pgg: Only Glide Reflections
Wallpapers with a group of symmetry pg also possess, apart from two translations in linearly independent directions, two glide reflections in parallel directions. The axis of each glide reflection is illustrated with a teal line.
Tilings with a group of symmetry pgg admit two glide reflections in different directions and two rotations of order two. The centre of the rotations is indicated with a hollow diamond.


Pm and Pmm: Reflection Symmetries, but No Glide Reflections
Similar to the previous two symmetry groups, we have wallpaper designs with group of symmetry pm and pmm. Tilings with groups of symmetry pm have two reflections, with axes in parallel directions. The blue lines represent the axes of such reflections.
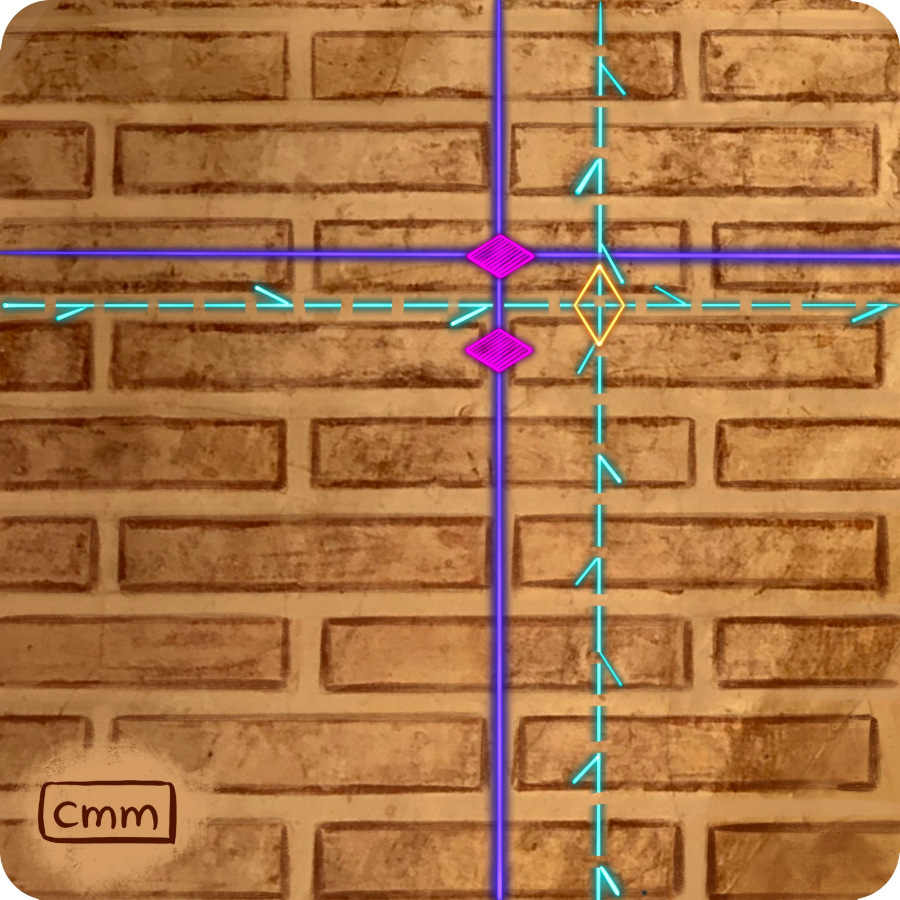
On the other hand, tilings with a group of symmetry pmm have a total of four reflections in two perpendicular directions. The points where the axes of the reflections intersect are centres of rotation of order two. Since there is a reflection passing through each one of these rotation centres, we denote it with a magenta diamond shape.


Symmetry Groups with Reflections and Glide Reflections
Tilings with a group of symmetry cm have one reflection and one glide reflection in parallel directions. They don’t have any rotation as symmetry.

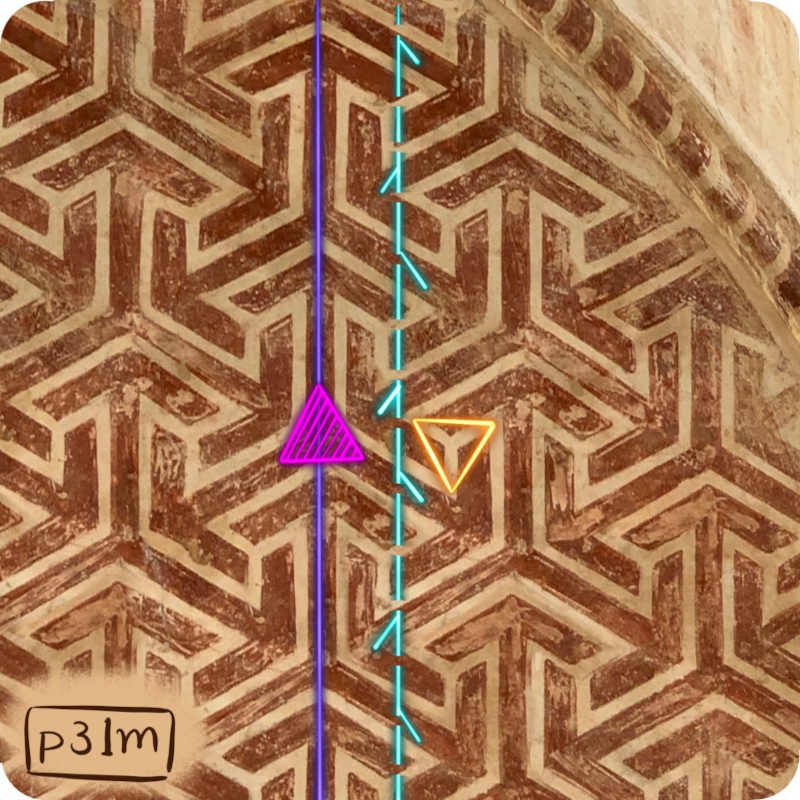
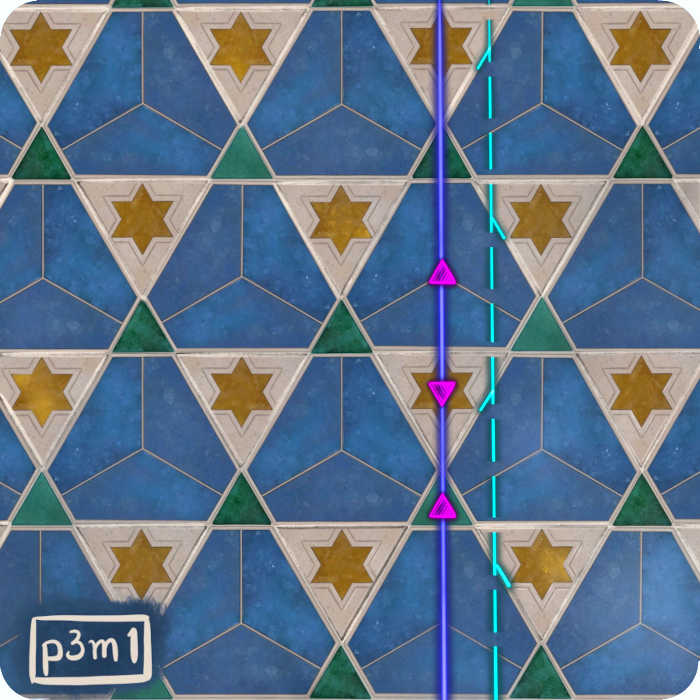
Tilings with groups of symmetry p31m and p3m1 are sometimes confused (and the code of the symmetry groups doesn’t really help) They both possess, like cm, one reflection, and one glide reflection in parallel directions. But in addition, they have rotations of order three. In the case of p31m, there are two rotations of order three, one of the centres passing through the axis of the reflection.
As for tilings with a group of symmetry p3m1, they have three rotations of order three, lying on the axis of the reflection.
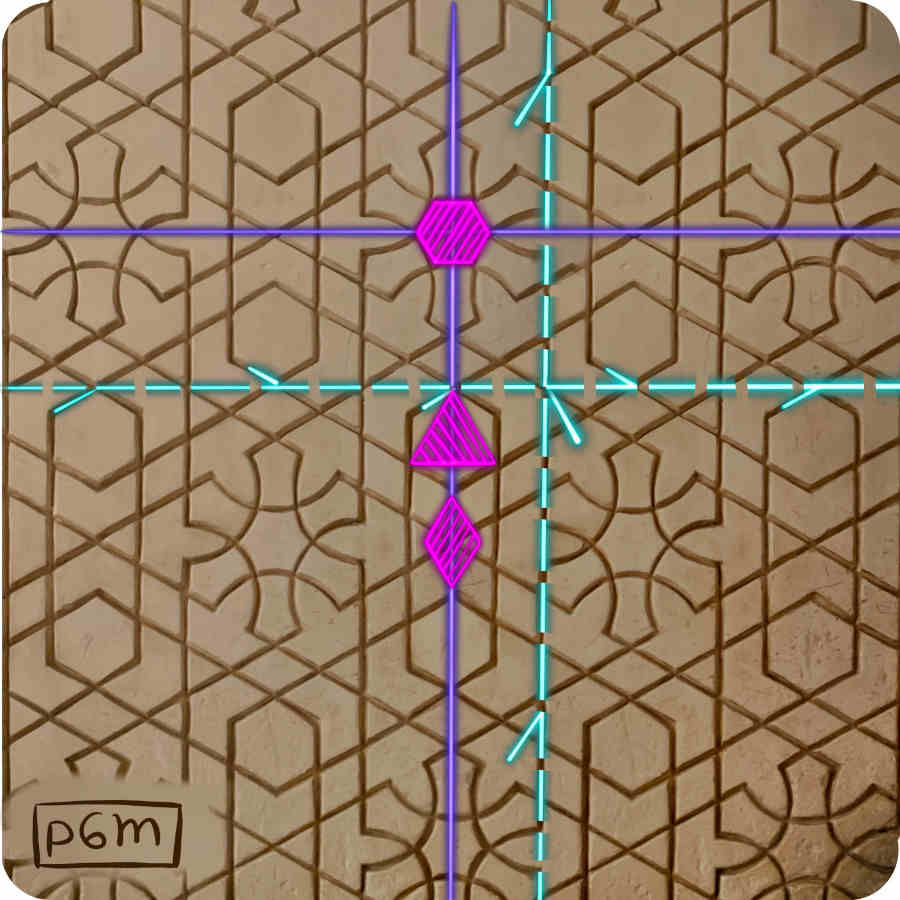
The triangles show the centres of rotations of order three. If the centre is on an axis of reflection, it is drawn as a magenta triangle. If not, then the triangle is hollow, with a gold outline.
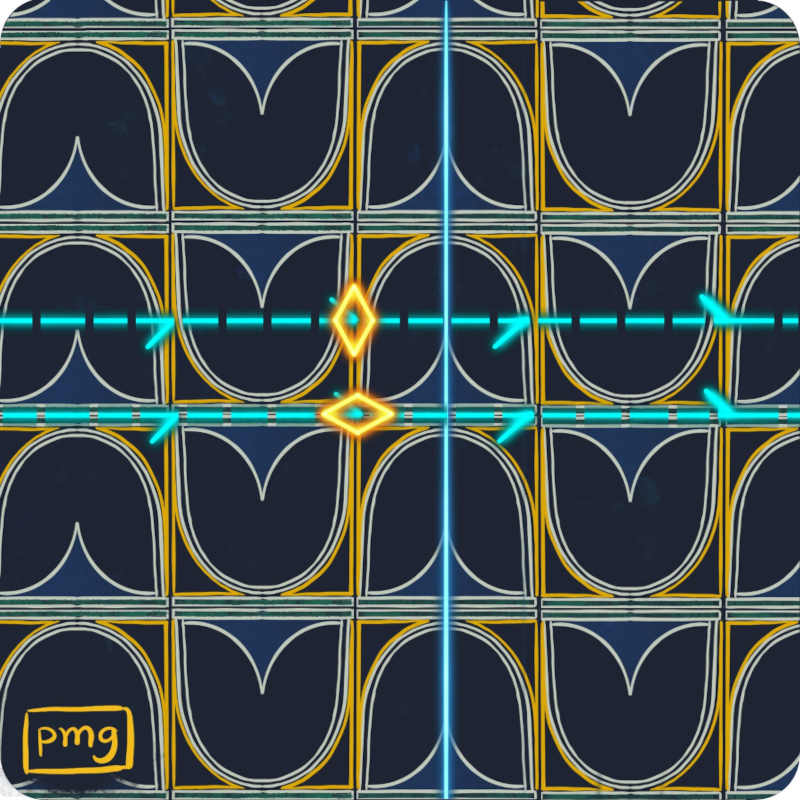
Wallpaper designs with a group of symmetry pmg have one reflection, two glide reflections perpendicular to the reflection, and two rotations of order two.
On the other hand, tilings with group of symmetry p4g have also one reflection and one glide reflection in perpendicular directions. Plus, they have another glide reflection, one rotation of order two, and one rotation of order four (the centre of this rotation is indicated by a square with a gold outline).

There are also crystallographic plane groups with more reflections and glide reflections. The groups cmm and p6m have two glide reflections and two reflections. As you can see, from the picture below, they come in pairs: a reflection and a glide reflection in parallel directions, while the other two (also parallel) are perpendicular to the first. The difference between these two groups comes from the rotations they allow. In the group cmm, there are three rotations of order two. In the group p6m there are three rotations: one of order two, one of order three, and one of order six.
And, if the wallpaper tiling has a group of symmetry p4m, then it has three reflections (two parallel) and a glide reflection (which, as you can observe from the drawing, is parallel to the third reflection). In addition, we have two rotations of order four and one rotation of order two.

Only rotations.
Finally, we have the tilings which, apart from the two translations in linearly independent directions, admit only rotations as symmetry: there are no reflections or glide reflections. Moreover, they have rotations of order either two, three, four, or six: that’s all. These crystallographic groups receive their code name depending on the highest rotation order: p2, p3, p4, and p6. Each one of them is illustrated below.

The Palace of Alhambra
I remember hearing about the Palace of Alhambra in Granada, Spain, when I took the class about tilings. When we covered the material about wallpaper tilings, someone said the 17-plane crystallographic groups are represented in Alhambra.
I was able to visit the Palace of Alhambra this summer, determined to find all 17 crystallographic groups. Our tour guide mentioned Edith Alice Müller, who studied patterns at the Alhambra for her doctoral thesis, back in 1943. The tour guide also spoke briefly about crystallographic groups and, looking me straight in the eye, repeated the story I once heard about the presence of the 17 crystallographic groups in the palace. I took as many photos as possible, amazed to see all those images that I once saw in photocopies of a book now live.

But while reviewing the photos on my way back to Seville, I noticed that I couldn’t find all the symmetry groups. The images of groups pgg, pmm, cm, p31m, p4g, cmm, p6m, p4m, p3, p4, and p6 (only 11 groups of crystallographic planes) correspond to the tilings I found in Alhambra. The tiling corresponding to the symmetry group p2 comes from Plaza de España in Seville. And the mosaic that I show with the symmetry group p1, I built it using a mosaic that I also found in Seville. The tiling with the symmetry group pmm comes from a collection of photographs I took on a trip to Puebla, Mexico, back in 2015, while the tiling corresponding to pg is found on some sidewalks in Heidelberg. The remaining two mosaics were created digitally.
I thought maybe I missed a few, given that I attended with a group, or maybe some of them are kept in a hidden spot under some restoration process. But then I came across several papers (including a note by Branko Grümbaum from 2006) about how it is unclear whether all crystallographic groups are indeed in Alhambra. Müller documented 12 of the 17 crystallographic groups, although, as Grümbaum points out, some writers claim Müller actually found 14 groups. The authors who claim that all 17 crystallographic plane groups can be found in Alhambra cite the book of José Maria Montesinos, Classical Tessellations and Three-Manifolds, published by Springer in 1987. Grümbaum points out, among other arguments that Montesinos considers, for some cases, the colouring of the tiles: that is, the symmetry groups sometimes are considered so that they not only preserve the shape of the tiles but the colour too. In that case, Grümbaum says, “it is easy to verify that by assigning appropriate colours, just two of the Alhambra mosaics could yield all seventeen groups”.
So, what do you think? Should colours also be preserved by the symmetries in a crystallographic group?
References:
- Fedorov, E (1891) “Симметрія на плоскости” (Simmetrija na ploskosti, Symmetry in the plane), Записки Императорского С.-Петербургского минералогического общества (Zapiski Imperatorskogo Sant-Petersburgskogo Mineralogicheskogo Obshchestva, Proceedings of the Imperial St. Petersburg Mineralogical Society), series 2, 28 : 345–390 (in Russian).
- Grünbaum, B., & Shephard, G. C. (1987). Tilings and patterns. Courier Dover Publications.
- Grünbaum, B. (2006). What symmetry groups are present in the Alhambra?. Notices of the AMS, 53(6), 670-673.
- Weisstein, E. W. “Wallpaper Groups.” From MathWorld – A Wolfram Web Resource. https://mathworld.wolfram.com/WallpaperGroups.html
Tags:
Mathematics
Groups
Symmetry