The Cosmic Web of Galaxies, Dark Matter and How It Emerged

The observable universe is rich in structures and patterns. From atomic nuclei to huge clusters of galaxies, it hosts a vast variety of shapes and complex phenomena. In many cases complex structures emerge from the collective action of simple physical processes as soon as many interacting constituents join to form a system. An example is the hexagonal geometry of snow crystals, which reflects the internal order of water molecules forming six-sided arrangements due to fundamental electric dipole-dipole interactions. On much larger length scales of around a few 10 to 100 million light-years, it is yet another simple, fundamental law of nature, that of gravity, and a particular set of initial conditions that lead to an intricate, web-like structured geometric pattern in the distribution of matter, known as the Cosmic Web.

In order to observe the Cosmic Web, we need to look far beyond our own galaxy, at length scales on which entire galaxies – with hundred billions of stars – appear like tiny particles. To put these scales into context, let us imagine “zooming out” out of the Solar System, adopting the perspective of an outside observer. As we pass the outer planets, we first note how long it takes even for a light ray to traverse interplanetary and interstellar distances. Nothing travels faster than light, with a velocity of nearly 300,000 km/s (that is ≈ 23 Earth diameters per second). Still, sunlight needs about eight minutes to reach Earth, four hours to Neptune, and four years to arrive at the closest star next to our own, Proxima Centauri. In comparison, NASA’s Voyager probes launched in 1977, the farthest human-made objects, travelling at 61,500 km/h and having left the Solar System by now, would need around 80,000 years to cover the distance to the next star.

Now think of all the stars visible to the bare eye at night – whose light we see only as tiny dots across the sky. The vast majority of these stars, however, occupies only a relatively “tiny” region of a few thousand light-years in radius around the Sun’s position in the Orion spiral arm of the Milky Way galaxy (see Fig. 1 below). For comparison, the total galaxy diameter is about 100,000 light-years. The Milky Way is itself gravitationally bound to a larger structure known as the Local Group, with a diameter of 10 million light-years. The Local Group in turn is embedded in the Local Supercluster – a collection of more than hundred individual groups and clusters of galaxies. The Local Supercluster has a total diameter of 110 million light-years, meaning the light we observe from some of its parts has been emitted at a time when dinosaurs inhabited Earth.

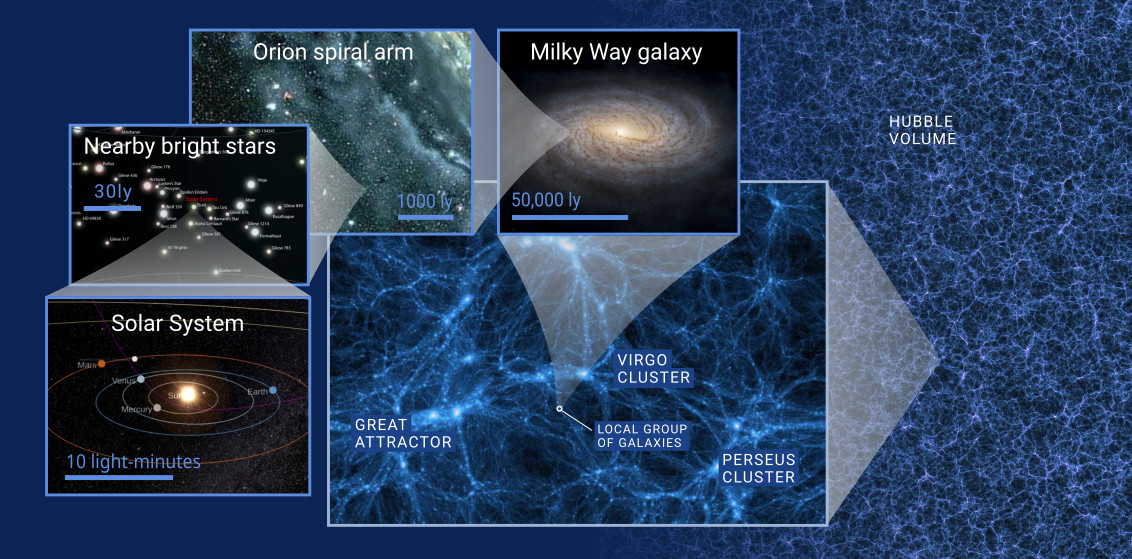
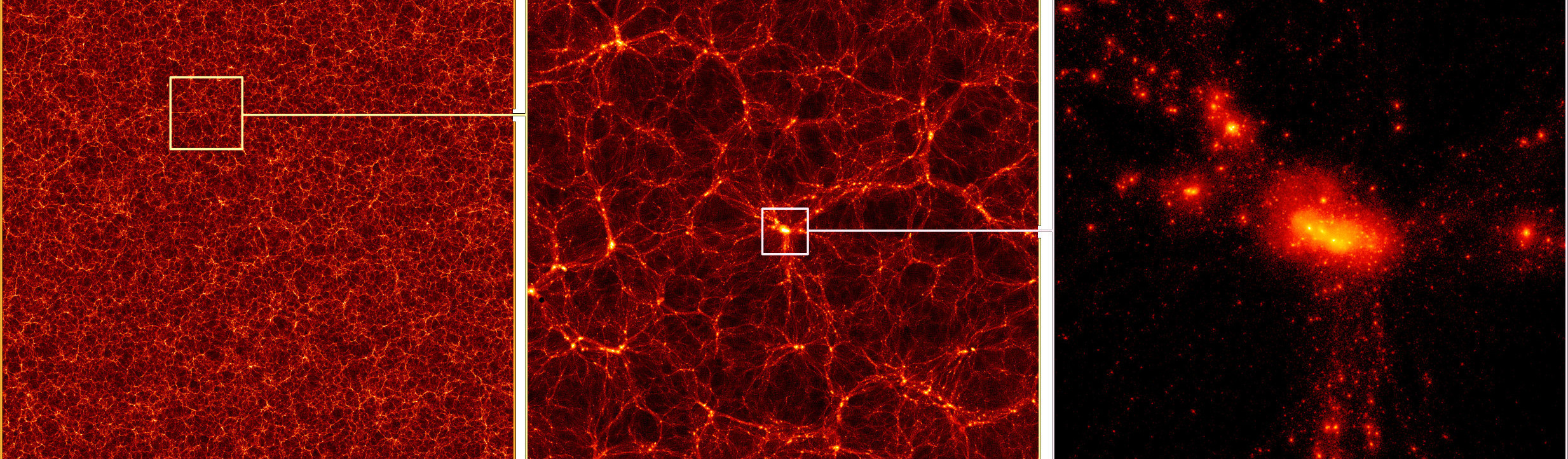
It is on these huge length scales that the cosmic matter distribution reveals an interesting shape. Instead of being randomly, uniformly scattered in space, galaxies are distributed along geometric patterns outlined by huge, tenuous filaments and planar features known as sheets (see Figs. 1, 2 and the article cover image). These filaments and sheets are separated by cosmic voids – vast regions nearly empty of galaxies. While prominent filaments can reach lengths of several 100 million light-years, voids have typical diameters between 30 and 300 million light-years. By far most of the cosmic volume turns out to be empty. In other places, where two or more large filaments intersect, the density of matter becomes so high that massive clusters of galaxies can form, which may contain hundreds or thousands of member galaxies. Being the lagest and most massive gravitationally bound objects in the universe, galaxy clusters represent the high-density “nodes” of the Cosmic Web. Along the filaments, clusters accrete new matter, meaning they are still in the process of growing. Nonetheless, by far most galaxies in the universe are found in little groups, like the Local Group, which is located in a filament connecting the Fornax cluster with the Virgo cluster of galaxies.

The Cosmic Web is the largest known coherent pattern of structures, pervading the entire known observable universe, integrating and connecting gravitationally bound physical structures such as galaxy clusters. Meanwhile, the Cosmic Web shares features similar to geometric spiderweb graphs, which can be strung up in equilibrium such that all strings are in tension. Its structural elements can be identified and approximated by vertices, edges, faces and cells of abstract models such as the Voronoi tessellation or generalisations of it. Observationally, the intricate structure of the Cosmic Web has been mapped systematically since the 1980s after the first detections of nearby filaments and voids. Over the past decades, enormous progress has been made in particular using large-scale galaxy redshift surveys such as the Sloan Digital Sky Survey, which have allowed to create detailed 3D maps of the spatial galaxy distribution in large parts of the cosmic volume around us. A recent example for such a map is shown in Fig. 2.

Large-scale galaxy maps as the one shown in Fig. 2 however reveal only a small part of the Cosmic Web: its luminous mass component. The Cosmic Web has a pronounced “dark side”, a component of dark matter that shares the same web-like geometric shape. Dark matter, an exotic substance not made from ordinary atoms, cannot be seen using telescopes, as it does not interact electromagnetically. Still, it can be made visible through gravity, as its presence affects the motion of stars, galaxies and even the paths of light rays (a phenomenon known as gravitational lensing). Systematic mass measurement techniques require the presence of dark matter in large amounts, and allow to map both its amount and spatial distribution. These methods find that dark matter forms extended clumps, so-called halos, embedding the visible stars and galaxies. Combining several independent observations implies that more than 85 percent of the matter in the universe is dark, hugely dominating gravitationally over the luminous matter. In fact, the gravity of dark matter keeps galaxies and clusters together in the first place, as without it, these systems would simply disperse on timescales around a billion years. Moreover, the luminous matter distribution turns out to closely follow that of dark matter for the same reason, at least on Cosmic Web scales. Thus we see galaxies in filaments or clusters only because dark matter has formed these structures, while the luminous matter simply follows dark matter’s gravitational attraction.

Structure Growth Out of Early Quantum Fluctuations

What is the origin of the Cosmic Web? How did it form and get its shape? Can we understand its shape based on fundamental physical laws or processes? If we wish to understand how cosmic structures have formed, whether dark or visible, we need to start by looking at the early universe shortly after the big bang. In particular, we need observations and a physical model telling us in what state the universe started and how it has since evolved in time, allowing to explain how we got from this initial state to the presently observed, richly structured universe. Both the initial state and the subsequent cosmic evolution turn out to be well known:

• The initial conditions of structure formation are probed with high accuracy and precision by observations of the Cosmic Microwave Background (CMB), the oldest light in the universe. The CMB is a thermal leftover radiation from the hot early stages of the cosmos, released when matter decoupled from photons and the universe became transparent. Thus photons could propagate almost freely without interactions with matter, conserving imprints of early structures on the radiation temperature. The emission time and physical properties of the CMB can be derived from simple theoretical considerations, and are confirmed to outstanding detail by all measurements. Observing this radiation today provides us with a “snapshot” of the early structures, from which we can infer a remarkably uniform past state of the universe, with gas fluctuations of order one part in 10⁵. Remarkably, the fluctuations are compatible with a realisation of a Gaussian Random Field, as is theoretically expected from models of so-called cosmic inflation, describing the quantum processes that likely created these fluctuations during the earliest moments of the universe.

• The subsequent growth of structures from these initial “seeds” of structure formation to the presently observed state is typically described (and well understood) within the theoretical context of an expanding universe that started with a big bang, described by General Relativity. The most prominent and widely assumed model is the by now firmly established Cosmological Standard Model. Any successful theory of structure formation furthermore needs to account for the unavoidable fact that the majority of matter in the universe is dark. At the same time, it needs to be stressed that model details such as the dark matter candidate are primarily required for quantitative predictions about the present-day structures. The mere emergence of filaments and voids, meanwhile, is not specific to many theoretical assumptions at all – not even to the law of gravity. For instance, in a modified gravity theory without dark matter, the growth of Gaussian fluctuations would lead to filamentary patterns as well. Thus we will keep the subsequent discussion as model-independent as possible, and the qualitative conclusions we will derive remain valid for any expanding universe in which gravity is present and the initial fluctuations are Gaussian.

So how did the tiny initial fluctuations in the cosmic matter density grow to become the present-day structures? The formation of cosmic large-scale structure requires a long-range force, and the only one available (that we know of) is gravity. Gravity in turn had to amplify any pre-existing irregularities in the matter distribution as it led to what is known as gravitational instability: in a spatially varying density distribution, regions denser than on cosmic average develop a net attraction drawing in material from the surroundings. This increases the imbalance (i.e. the density contrast) between the regions even further, resulting in even stronger gravitational attraction. This self-amplifying process would in principle be exponential if it was not for a damping effect due to the cosmic expansion. Once the overdensity in a local region exceeds a certain ratio to the cosmic average, that region decouples from the cosmic expansion and collapses under its own gravity. Initially underdense regions, in contrast, turn rather quickly into voids as they get emptied by gravity.

Structure Formation in a Dark Universe

Dark matter plays a decisive role in cosmic structure formation. It is required to quantitatively explain the growth that led to the large density contrasts in present-day structures such as galaxies and clusters. Without a non-electromagnetically interacting matter component, the fluctuations probed by the CMB would not have been able to evolve into the observed galaxies during the time that has passed since decoupling. The key aspect to understanding this growth is that, since dark matter particles were not coupled to photons, dark matter fluctuations could grow denser and more massive even before the release of the CMB – whereas the growth of ordinary matter fluctuations was inhibited by radiation. Therefore, dark matter fluctuations provided the first seeds and the sites for the formation of luminous structures such as stars and galaxies.

From Zel’dovich Pancakes to Filaments

Now that we know how density fluctuations got amplified, how and why did filaments and sheet form rather than more or less isotropic clumps? Here is where the Gaussian shape of the initial conditions, and the fact that gravity amplifies anisotropies, get important. Already very simple analytic models for the motion of particles under the influence of gravity in an expanding background allow to understand the key features of this process on a qualitative level. Pioneered by Yakov B. Zel’dovich in the 1960s/70s, a particularly beautiful and intuitive method that allows to understand the emergence of filaments and sheets is the Zel’dovich approximation. In it, particles are treated as if they kept drifting along straight lines with their initial velocities set by the initial density distribution and its gravitational potential. Initially overdense regions produce convergent mass flows, while underdense regions lead to divergent ones. The density field at later times is then calculated from the motion of mass elements. Locally, the density in- or decreases as the matter flows contract or expand. The deformation of a matter flow is quantified by the Zel’dovich deformation tensor, whose eigenvalues determine how a local density perturbation is going to evolve.

This conceptually simple idealisation already leads to interesting predictions. One is that the evolution results in the formation of caustic lines, i.e. lines on which the density field formally assumes infinite values, when mass elements from two or more different initial locations arrive at the same final location. A second important prediction is that the formation of structures must be generally anisotropic because the eigenvalues of the deformation tensor cannot be assumed to be all equal – which would be required for a spherical collapse. In particular, it was pointed out by Doroshkevich in 1970 that if the initial density contrast is a Gaussian Random Field, the eigenvalues of the Zel’dovich tensor will have zero probability of being pairwise equal. Thus Gaussian initial conditions forbid isotropic structure growth. Instead, overdense clouds of particles collapse along their shortest axis (given by the third eigenvalue) first, forming oblate regions known as Zel’dovich pancakes. These pancakes in turn contract along the axis of the second-largest eigenvalue, leading to quasi-1D features, the filaments, that finally shrink into compact clumps (halos or vertices) as soon as all three eigenvalues have passed a singularity. In this sense, structure growth can be described as a process of dimensionality reduction, i.e. matter collapsing to form progressively lower-dimensional features.

Qualitatively, the conclusions derived from the Zel’dovich approximation are confirmed to remarkable accuracy by the results of direct numerical modelling using large-scale cosmological N-body simulations such as the Millennium run. At a certain point, the Zel’dovich approximation breaks down, signalling the importance of higher-order effects of gravitational collapse. Still, an important insight it offers is the generality under which anisotropic structures such as filaments and sheets emerge. The pronounced anisotropy results from initial conditions that get amplified by gravity. Remarkably, the evolution of particles on Zel’dovich trajectories is strictly speaking not specific to the law of gravity, or to the fact that gravity provides the growth at all – but rather to the presence of Gaussian velocity potentials. These arise also in other contexts. The Zel’dovich formalism for instance uses concepts known from optics, and the nature of the caustic “skeleton” of the Cosmic Web can be understood well within singularity theory. The mechanism by which water in a swimming pool forms (optical) caustic patterns is the same as that responsible for the cosmic filaments.

Still, the dynamics driven by gravity do play a decisive role for the properties of the Cosmic Web in two ways. The large-scale component of gravity on the one hand amplifies the already present anisotropies. On the other hand, small-scale gravitational fields start to cause pronounced deviations from the extrapolated trajectories of the Zel’dovich evolution. These details become important especially on the scales of galaxy and cluster formation, whose complicated details we bypassed in this article, as we focused specifically on the large-scale features of the Cosmic Web. During the further evolution, gravity holds galaxies, clusters and filaments together and maps the Cosmic Web into its present shape. It is during this evolution that the details of dark matter and the cosmic expansion do become relevant after all. For instance, in the observationally favoured Cold Dark Matter model, smaller structures progressively form bigger structures by accretion and merging – a process known as hierarchical (bottom-up) structure formation, whose predictions for the statistical properties of the Cosmic Web differ significantly from alternative models. This is what makes the study of cosmic structure formation important even when we wish to answer questions about the universe itself or the fundamental nature of its constituents.

The formation and evolution of cosmic structure is one of the key issues in cosmology, given that fundamental questions of physics, astronomy and cosmology are very tightly linked to it. Whereas the emergence of filaments and voids is a very general outcome, the exact statistical properties of the Cosmic Web and their evolution over cosmic history depend crucially on theoretical assumptions of the structure formation model. Comparing theoretical predictions with present-day observations reveals key insights to a large number of fundamental unsolved questions of our cosmos. This is one of the main reasons why it is so important that we understand how we get from simple initial conditions to a complex, richly structured universe.

Acknowledgement: I would like to thank Sara Marcos Plaza, Matthias Bartelmann, Manfred Salmhofer, Sara Konrad, Aletta Berger and the whole STRUCTURES blog team for valuable discussions, comments and input during the writing process of this article.